Matrex v0.6.8 Matrex View Source

Performs fast operations on matrices using native C code and CBLAS library.

Access behaviour

Access behaviour is partly implemented for Matrex, so you can do:


    iex> m = Matrex.magic(3)
    #Matrex[3×3]
    ┌                         ┐
    │     8.0     1.0     6.0 │
    │     3.0     5.0     7.0 │
    │     4.0     9.0     2.0 │
    └                         ┘
    iex> m[2][3]
    7.0

Or even:


    iex> m[1..2]
    #Matrex[2×3]
    ┌                         ┐
    │     8.0     1.0     6.0 │
    │     3.0     5.0     7.0 │
    └                         ┘

There are also several shortcuts for getting dimensions of matrix:


    iex> m[:rows]
    3

    iex> m[:size]
    {3, 3}

calculating maximum value of the whole matrix:


    iex> m[:max]
    9.0

or just one of it's rows:


    iex> m[2][:max]
    7.0

calculating one-based index of the maximum element for the whole matrix:


    iex> m[:argmax]
    8

and a row:


    iex> m[2][:argmax]
    3

Inspect protocol

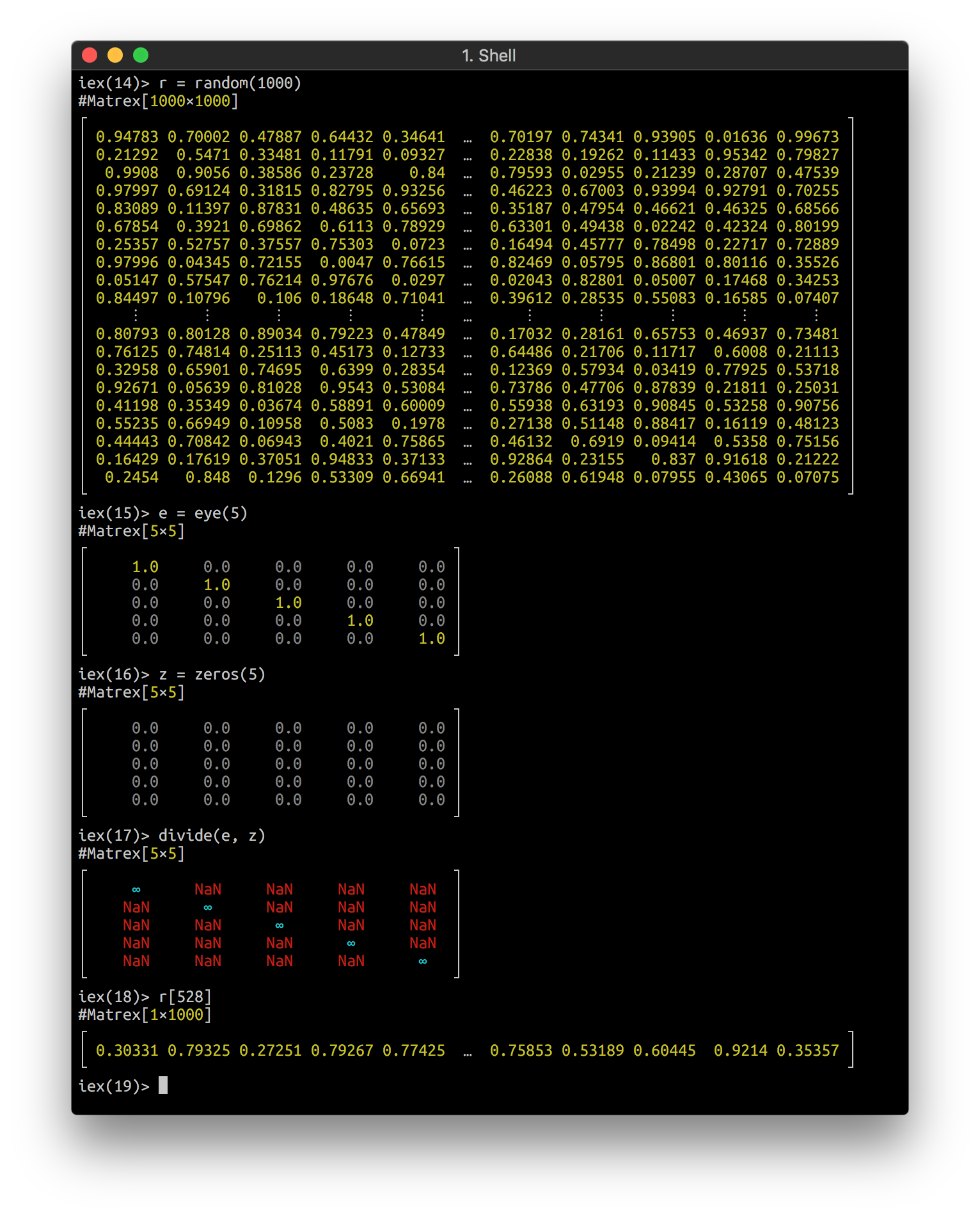
Matrex implements Inspect and looks nice in your console:

Inspect Matrex

Math operators overloading

Matrex.Operators module redefines Kernel math operators (+, -, *, / <|>) and defines some convenience functions, so you can write calculations code in more natural way.

It should be used with great caution. We suggest using it only inside specific functions and only for increased readability, because using Matrex module functions, especially ones which do two or more operations at one call, are 2-3 times faster.

Example


    def lr_cost_fun_ops(%Matrex{} = theta, {%Matrex{} = x, %Matrex{} = y, lambda} = _params)
        when is_number(lambda) do
      # Turn off original operators
      import Kernel, except: [-: 1, +: 2, -: 2, *: 2, /: 2, <|>: 2]
      import Matrex.Operators
      import Matrex

      m = y[:rows]

      h = sigmoid(x * theta)
      l = ones(size(theta)) |> set(1, 1, 0.0)

      j = (-t(y) * log(h) - t(1 - y) * log(1 - h) + lambda / 2 * t(l) * pow2(theta)) / m

      grad = (t(x) * (h - y) + (theta <|> l) * lambda) / m

      {scalar(j), grad}
    end

The same function, coded with module methods calls (2.5 times faster):

    def lr_cost_fun(%Matrex{} = theta, {%Matrex{} = x, %Matrex{} = y, lambda} = _params)
        when is_number(lambda) do
      m = y[:rows]

      h = Matrex.dot_and_apply(x, theta, :sigmoid)
      l = Matrex.ones(theta[:rows], theta[:cols]) |> Matrex.set(1, 1, 0)

      regularization =
        Matrex.dot_tn(l, Matrex.square(theta))
        |> Matrex.scalar()
        |> Kernel.*(lambda / (2 * m))

      j =
        y
        |> Matrex.dot_tn(Matrex.apply(h, :log), -1)
        |> Matrex.subtract(
          Matrex.dot_tn(
            Matrex.subtract(1, y),
            Matrex.apply(Matrex.subtract(1, h), :log)
          )
        )
        |> Matrex.scalar()
        |> (fn
              :nan -> :nan
              x -> x / m + regularization
            end).()

      grad =
        x
        |> Matrex.dot_tn(Matrex.subtract(h, y))
        |> Matrex.add(Matrex.multiply(theta, l), 1.0, lambda)
        |> Matrex.divide(m)

      {j, grad}
    end

Enumerable protocol

Matrex implements Enumerable, so, all kinds of Enum functions are applicable:


    iex> Enum.member?(m, 2.0)
    true

    iex> Enum.count(m)
    9

    iex> Enum.sum(m)
    45

For functions, that exist both in Enum and in Matrex it's preferred to use Matrex version, beacuse it's usually much, much faster. I.e., for 1 000 x 1 000 matrix Matrex.sum/1 and Matrex.to_list/1 are 438 and 41 times faster, respectively, than their Enum counterparts.

Saving and loading matrix

You can save/load matrix with native binary file format (extra fast) and CSV (slow, especially on large matrices).

Matrex CSV format is compatible with GNU Octave CSV output, so you can use it to exchange data between two systems.

Example


    iex> Matrex.random(5) |> Matrex.save("rand.mtx")
    :ok
    iex> Matrex.load("rand.mtx")
    #Matrex[5×5]
    ┌                                         ┐
    │ 0.05624 0.78819 0.29995 0.25654 0.94082 │
    │ 0.50225 0.22923 0.31941  0.3329 0.78058 │
    │ 0.81769 0.66448 0.97414 0.08146 0.21654 │
    │ 0.33411 0.59648 0.24786 0.27596 0.09082 │
    │ 0.18673 0.18699 0.79753 0.08101 0.47516 │
    └                                         ┘
    iex> Matrex.magic(5) |> Matrex.divide(Matrex.eye(5)) |> Matrex.save("nan.csv")
    :ok
    iex> Matrex.load("nan.csv")
    #Matrex[5×5]
    ┌                                         ┐
    │    16.0     ∞       ∞       ∞       ∞   │
    │     ∞       4.0     ∞       ∞       ∞   │
    │     ∞       ∞      12.0     ∞       ∞   │
    │     ∞       ∞       ∞      25.0     ∞   │
    │     ∞       ∞       ∞       ∞       8.0 │
    └                                         ┘

NaN and Infinity

Float special values, like :nan and :inf live well inside matrices, can be loaded from and saved to files. But when getting them into Elixir they are transferred to :nan,:inf and :neg_inf atoms, because BEAM does not accept special values as valid floats.

    iex> m = Matrex.eye(3)
    #Matrex[3×3]
    ┌                         ┐
    │     1.0     0.0     0.0 │
    │     0.0     1.0     0.0 │
    │     0.0     0.0     1.0 │
    └                         ┘

    iex> n = Matrex.divide(m, Matrex.zeros(3))
    #Matrex[3×3]
    ┌                         ┐
    │     ∞      NaN     NaN  │
    │    NaN      ∞      NaN  │
    │    NaN     NaN      ∞   │
    └                         ┘

    iex> n[1][1]
    :inf

    iex> n[1][2]
    :nan

Link to this section Summary

Types

element()

index()

matrex()

t()

Functions

add(a, b)

Adds scalar to matrix.

add(matrex1, matrex2, alpha \\ 1.0, beta \\ 1.0)

Adds two matrices or scalar to each element of matrix. NIF.

apply(matrix, function_atom)

Applies given function to each element of the matrix and returns the matrex of results. NIF.

apply(arg1, arg2, function)

Applies function to elements of two matrices and returns matrix of function results.

argmax(matrex)

Returns one-based index of the biggest element. NIF.

at(arg, row, col)

Get element of a matrix at given one-based (row, column) position.

cholesky(arg)

Matrix cholesky decompose. NIF, via naive implementation.

column(arg, col)

Get column of matrix as matrix (vector) in matrex form. One-based.

column_to_list(matrex, column)

Get column of matrix as list of floats. One-based, NIF.

concat(list_of_ma)

Concatenate list of matrices along columns.

concat(matrex1, matrex2, type \\ :columns)

Concatenate two matrices along rows or columns. NIF.

contains?(matrex, value)

Checks if given element exists in the matrix.

diagonal(matrix)

Create new matrix with only diagonal elements from a given matrix.

divide(dividend, divisor)

Divides two matrices element-wise or matrix by scalar or scalar by matrix. NIF through find/2.

dot(arg1, arg2)

Matrix multiplication. NIF, via cblas_sgemm().

dot_and_add(arg1, arg2, matrex)

Matrix multiplication with addition of third matrix. NIF, via cblas_sgemm().

dot_and_apply(arg1, arg2, function)

Computes dot product of two matrices, then applies math function to each element of the resulting matrix.

dot_nt(arg1, arg2)

Matrix multiplication where the second matrix needs to be transposed. NIF, via cblas_sgemm().

dot_tn(arg1, arg2, alpha \\ 1.0)

Matrix dot multiplication where the first matrix needs to be transposed. NIF, via cblas_sgemm().

eye(size, value \\ 1.0)

Create eye (identity) square matrix of given size.

fill(size, value)

Create square matrix filled with given value. Inlined.

fill(rows, cols, value)

Create matrix filled with given value. NIF.

find(matrex, value)

Find position of the first occurence of the given value in the matrix. NIF.

first(arg)

Return first element of a matrix.

forward_substitute(arg1, arg2)

Matrix forward substitution. NIF, via naive C implementation.

get(matrex, key, default)

heatmap(matrex, type \\ :mono256, opts \\ [])

Prints monochrome or color heatmap of the matrix to the console.

identity(size)

An alias for eye/1.

list_of_rows(arg)

Returns list of all rows of a matrix as single-row matrices.

list_of_rows(arg1, arg2)

Returns range of rows of a matrix as list of 1-row matrices.

load(file_name)

Load matrex from file.

load(file_name, format)

magic(n)

Creates "magic" n*n matrix, where sums of all dimensions are equal.

max(matrex)

Maximum element in a matrix. NIF.

max_finite(matrex)

Returns maximum finite element of a matrex. NIF.

min(matrex)

Minimum element in a matrix. NIF.

min_finite(matrex)

Returns minimum finite element of a matrex. NIF.

multiply(scalar, scalar)

Elementwise multiplication of two matrices or matrix and a scalar. NIF.

neg(matrex)

Negates each element of the matrix. NIF.

new(lol_of_ma)

Creates new matrix from list of lists or text representation (compatible with MathLab/Octave).

new(rows, columns, function)

Creates new matrix with values provided by the given function.

normalize(matrex)

Bring all values of matrix into [0, 1] range. NIF.

ones(size)

Create matrex of ones of square dimensions or consuming output of size/1 function.

ones(rows, cols)

Create matrix filled with ones.

print(matrex, opts \\ [rows: 21])

Prints matrix to the console.

random(size)

Create square matrix of random floats.

random(rows, columns)

Create matrix of random floats in [0, 1] range. NIF.

reshape(enum, rows, columns)

Reshapes list of values into a matrix of given size or changes the shape of existing matrix.

resize(matrex, scale, method \\ :nearest)

Resize matrix by scaling its dimenson with scale. NIF.

row(arg, row)

Get row of matrix as matrix (vector) in matrex form. One-based.

row_to_list(matrex, row)

Return matrix row as list by one-based index.

save(matrex, file_name)

Saves matrex into file.

scalar(matrex)

Transfer one-element matrix to a scalar value.

set(arg, row, column, value)

Set element of matrix at the specified position (one-based) to new value.

set_column(arg1, column, arg2)

Set column of a matrix to the values from the given 1-column matrix. NIF.

size(arg)

Return size of matrix as {rows, cols}

square(matrex)

Produces element-wise squared matrix. NIF through multiply/4.

submatrix(matrex, rows, cols)

Returns submatrix for a given matrix. NIF.

subtract(scalar, scalar)

Subtracts two matrices or matrix from scalar element-wise. NIF.

subtract_inverse(first, second)

Subtracts the second matrix or scalar from the first. Inlined.

sum(matrex)

Sums all elements. NIF.

to_column(m)

Convert any matrix m×n to a column matrix (m*n)×1.

to_list(matrex)

Converts to flat list. NIF.

to_list_of_lists(matrex)

Converts to list of lists. NIF.

to_row(m)

Convert any matrix m×n to a row matrix 1×(m*n).

trace(matrex)

Trace of matrix (sum of all diagonal elements). Elixir.

transpose(m)

Transposes a matrix. NIF.

update(arg, row, col, fun)

Updates the element at the given position in matrix with function.

zeros(size)

Create square matrix of size size rows × size columns, filled with zeros. Inlined.

zeros(rows, cols)

Create matrix of zeros of the specified size. NIF, using memset().

Link to this section Types

element()

element() :: number() | :nan | :inf | :neg_inf

index()

index() :: pos_integer()

matrex()

matrex() :: %Matrex{data: binary()}

t()

t() :: matrex()

Link to this section Functions

add(a, b)

add(matrex(), number()) :: matrex()

add(number(), matrex()) :: matrex()

Adds scalar to matrix.

See Matrex.add/4 for details.

add(matrex1, matrex2, alpha \\ 1.0, beta \\ 1.0)

add(matrex(), matrex(), number(), number()) :: matrex()

Adds two matrices or scalar to each element of matrix. NIF.

Can optionally scale any of the two matrices.

C = αA + βB

Raises ErlangError if matrices' sizes do not match.

Examples

iex> Matrex.add(Matrex.new([[1,2,3],[4,5,6]]), Matrex.new([[7,8,9],[10,11,12]]))
#Matrex[2×3]
┌                         ┐
│     8.0    10.0    12.0 │
│    14.0    16.0    18.0 │
└                         ┘

Adding with scalar:

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.add(m, 1)
#Matrex[3×3]
┌                         ┐
│     9.0     2.0     7.0 │
│     4.0     6.0     8.0 │
│     5.0    10.0     3.0 │
└                         ┘

With scaling each matrix:

iex> Matrex.add(Matrex.new("1 2 3; 4 5 6"), Matrex.new("3 2 1; 6 5 4"), 2.0, 3.0)
#Matrex[2×3]
┌                         ┐
│     11.0    10.0    9.0 │
│     26.0    25.0   24.0 │
└                         ┘

apply(matrix, function_atom)

apply(
  matrex(),
  atom()
  | (element() -> element())
  | (element(), index() -> element())
  | (element(), index(), index() -> element())
) :: matrex()

Applies given function to each element of the matrix and returns the matrex of results. NIF.

If second argument is an atom, then applies C language math function.

Example

iex> Matrex.magic(5) |> Matrex.apply(:sigmoid)
#Matrex[5×5]
┌                                         ┐
│-0.95766-0.53283 0.28366  0.7539 0.13674 │
│-0.99996-0.65364 0.96017 0.90745 0.40808 │
│-0.98999-0.83907 0.84385  0.9887-0.54773 │
│-0.91113 0.00443 0.66032  0.9912-0.41615 │
│-0.75969-0.27516 0.42418  0.5403 -0.1455 │
└                                         ┘

The following math functions from C are supported, and also a sigmoid function:

  :exp, :exp2, :sigmoid, :expm1, :log, :log2, :sqrt, :cbrt, :ceil, :floor, :truncate, :round,
  :abs, :sin, :cos, :tan, :asin, :acos, :atan, :sinh, :cosh, :tanh, :asinh, :acosh, :atanh,
  :erf, :erfc, :tgamma, :lgamm

If second argument is a function that takes one argument, then this function receives the element of the matrix.

Example

iex> Matrex.magic(5) |> Matrex.apply(&:math.cos/1)
#Matrex[5×5]
┌                                         ┐
│-0.95766-0.53283 0.28366  0.7539 0.13674 │
│-0.99996-0.65364 0.96017 0.90745 0.40808 │
│-0.98999-0.83907 0.84385  0.9887-0.54773 │
│-0.91113 0.00443 0.66032  0.9912-0.41615 │
│-0.75969-0.27516 0.42418  0.5403 -0.1455 │
└                                         ┘

If second argument is a function that takes two arguments, then this function receives the element of the matrix and its one-based index.

Example

iex> Matrex.ones(5) |> Matrex.apply(fn val, index -> val + index end)
#Matrex[5×5]
┌                                         ┐
│     2.0     3.0     4.0     5.0     6.0 │
│     7.0     8.0     9.0    10.0    11.0 │
│    12.0    13.0    14.0    15.0    16.0 │
│    17.0    18.0    19.0    20.0    21.0 │
│    22.0    23.0    24.0    25.0    26.0 │
└                                         ┘

If second argument is a function that takes three arguments, then this function receives the element of the matrix one-based row index and one-based column index of the element.

Example

iex> Matrex.ones(5) |> Matrex.apply(fn val, row, col -> val + row + col end)
#Matrex[5×5]
┌                                         ┐
│     3.0     4.0     5.0     6.0     7.0 │
│     4.0     5.0     6.0     7.0     8.0 │
│     5.0     6.0     7.0     8.0     9.0 │
│     6.0     7.0     8.0     9.0    10.0 │
│     7.0     8.0     9.0    10.0    11.0 │
└                                         ┘

apply(arg1, arg2, function)

apply(matrex(), matrex(), (element(), element() -> element())) :: matrex()

Applies function to elements of two matrices and returns matrix of function results.

Matrices must be of the same size.

Example

iex(11)> Matrex.apply(Matrex.random(5), Matrex.random(5), fn x1, x2 -> min(x1, x2) end)
#Matrex[5×5]
┌                                         ┐
│ 0.02025 0.15055 0.69177 0.08159 0.07237 │
│ 0.03252 0.14805 0.03627  0.1733 0.58721 │
│ 0.10865 0.49192 0.12166  0.0573 0.66522 │
│ 0.13642 0.23838 0.14403 0.57151 0.12359 │
│ 0.12877 0.12745 0.10933 0.27281 0.35957 │
└                                         ┘

argmax(matrex)

argmax(matrex()) :: index()

Returns one-based index of the biggest element. NIF.

There is also matrex[:argmax] shortcut for this function.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.argmax(m)
7

at(arg, row, col)

at(matrex(), index(), index()) :: element()

Get element of a matrix at given one-based (row, column) position.

Negative or out of bound indices will raise an exception.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.at(m, 3, 2)
9.0

You can use Access behaviour square brackets for the same purpose, but it will be slower:

iex> m[3][2]
9.0

cholesky(arg)

cholesky(matrex()) :: matrex()

Matrix cholesky decompose. NIF, via naive implementation.

The first matrix must be symmetric and positive definitive.

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[3, 4, 3], [4, 8, 6], [3, 6, 9]]) |>
...> Matrex.cholesky()
#Matrex[3×3]
┌                         ┐
│ 1.73205     0.0     0.0 │
│  2.3094 1.63299     0.0 │
│ 1.73205 1.22474 2.12132 │
└                         ┘

column(arg, col)

column(matrex(), index()) :: matrex()

Get column of matrix as matrix (vector) in matrex form. One-based.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.column(m, 2)
#Matrex[3×1]
┌         ┐
│     1.0 │
│     5.0 │
│     9.0 │
└         ┘

column_to_list(matrex, column)

column_to_list(matrex(), index()) :: [element()]

Get column of matrix as list of floats. One-based, NIF.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.column_to_list(m, 3)
[6.0, 7.0, 2.0]

concat(list_of_ma)

concat([matrex()]) :: matrex()

Concatenate list of matrices along columns.

The number of rows must be equal.

Example

iex> Matrex.concat([Matrex.fill(2, 0), Matrex.fill(2, 1), Matrex.fill(2, 2)])                #Matrex[2×6]
┌                                                 ┐
│     0.0     0.0     1.0     1.0     2.0     2.0 │
│     0.0     0.0     1.0     1.0     2.0     2.0 │
└                                                 ┘

concat(matrex1, matrex2, type \\ :columns)

concat(matrex(), matrex(), :columns | :rows) :: matrex()

Concatenate two matrices along rows or columns. NIF.

The number of rows or columns must be equal.

Examples

iex> m1 = Matrex.new([[1, 2, 3], [4, 5, 6]])
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘
iex> m2 = Matrex.new([[7, 8, 9], [10, 11, 12]])
#Matrex[2×3]
┌                         ┐
│     7.0     8.0     9.0 │
│    10.0    11.0    12.0 │
└                         ┘
iex> Matrex.concat(m1, m2)
#Matrex[2×6]
┌                                                 ┐
│     1.0     2.0     3.0     7.0     8.0     9.0 │
│     4.0     5.0     6.0    10.0    11.0    12.0 │
└                                                 ┘
iex> Matrex.concat(m1, m2, :rows)
#Matrex[4×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
│     7.0     8.0     9.0 │
│    10.0    11.0    12.0 │
└                         ┘

contains?(matrex, value)

contains?(matrex(), element()) :: boolean()

Checks if given element exists in the matrix.

Example

iex> m = Matrex.new("1 NaN 3; Inf 10 23")
#Matrex[2×3]
┌                         ┐
│     1.0    NaN      3.0 │
│     ∞      10.0    23.0 │
└                         ┘
iex> Matrex.contains?(m, 1.0)
true
iex> Matrex.contains?(m, :nan)
true
iex> Matrex.contains?(m, 9)
false

diagonal(matrix)

diagonal(matrex()) :: matrex()

Create new matrix with only diagonal elements from a given matrix.

Examples

iex> Matrex.eye(3) |> Matrex.diagonal()
┌                         ┐
│    1.0      1.0     1.0 │
└                         ┘

divide(dividend, divisor)

divide(matrex(), matrex()) :: matrex()

divide(matrex(), number()) :: matrex()

divide(number(), matrex()) :: matrex()

Divides two matrices element-wise or matrix by scalar or scalar by matrix. NIF through find/2.

Raises ErlangError if matrices' sizes do not match.

Examples

iex> Matrex.new([[10, 20, 25], [8, 9, 4]])
...> |> Matrex.divide(Matrex.new([[5, 10, 5], [4, 3, 4]]))
#Matrex[2×3]
┌                         ┐
│     2.0     2.0     5.0 │
│     2.0     3.0     1.0 │
└                         ┘

iex> Matrex.new([[10, 20, 25], [8, 9, 4]])
...> |> Matrex.divide(2)
#Matrex[2×3]
┌                         ┐
│     5.0    10.0    12.5 │
│     4.0     4.5     2.0 │
└                         ┘

iex> Matrex.divide(100, Matrex.new([[10, 20, 25], [8, 16, 4]]))
#Matrex[2×3]
┌                         ┐
│    10.0     5.0     4.0 │
│    12.5    6.25    25.0 │
└                         ┘

dot(arg1, arg2)

dot(matrex(), matrex()) :: matrex()

Matrix multiplication. NIF, via cblas_sgemm().

Number of columns of the first matrix must be equal to the number of rows of the second matrix.

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.dot(Matrex.new([[1, 2], [3, 4], [5, 6]]))
#Matrex[2×2]
┌                 ┐
│    22.0    28.0 │
│    49.0    64.0 │
└                 ┘

dot_and_add(arg1, arg2, matrex)

dot_and_add(matrex(), matrex(), matrex()) :: matrex()

Matrix multiplication with addition of third matrix. NIF, via cblas_sgemm().

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.dot_and_add(Matrex.new([[1, 2], [3, 4], [5, 6]]), Matrex.new([[1, 2], [3, 4]]))
#Matrex[2×2]
┌                 ┐
│    23.0    30.0 │
│    52.0    68.0 │
└                 ┘

dot_and_apply(arg1, arg2, function)

dot_and_apply(matrex(), matrex(), atom()) :: matrex()

Computes dot product of two matrices, then applies math function to each element of the resulting matrix.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.dot_and_apply(Matrex.new([[1, 2], [3, 4], [5, 6]]), :sqrt)
#Matrex[2×2]
┌                 ┐
│ 4.69042  5.2915 │
│     7.0     8.0 │
└                 ┘

dot_nt(arg1, arg2)

dot_nt(matrex(), matrex()) :: matrex()

Matrix multiplication where the second matrix needs to be transposed. NIF, via cblas_sgemm().

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.dot_nt(Matrex.new([[1, 3, 5], [2, 4, 6]]))
#Matrex[2×2]
┌                 ┐
│    22.0    28.0 │
│    49.0    64.0 │
└                 ┘

dot_tn(arg1, arg2, alpha \\ 1.0)

dot_tn(matrex(), matrex(), number()) :: matrex()

Matrix dot multiplication where the first matrix needs to be transposed. NIF, via cblas_sgemm().

The result is multiplied by scalar alpha.

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[1, 4], [2, 5], [3, 6]]) |>
...> Matrex.dot_tn(Matrex.new([[1, 2], [3, 4], [5, 6]]))
#Matrex[2×2]
┌                 ┐
│    22.0    28.0 │
│    49.0    64.0 │
└                 ┘

eye(size, value \\ 1.0)

eye(index(), element()) :: matrex()

Create eye (identity) square matrix of given size.

Examples

iex> Matrex.eye(3)
#Matrex[3×3]
┌                         ┐
│     1.0     0.0     0.0 │
│     0.0     1.0     0.0 │
│     0.0     0.0     1.0 │
└                         ┘

iex> Matrex.eye(3, 2.95)
#Matrex[3×3]
┌                         ┐
│    2.95     0.0     0.0 │
│     0.0    2.95     0.0 │
│     0.0     0.0    2.95 │
└                         ┘

fill(size, value)

fill(index(), element()) :: matrex()

Create square matrix filled with given value. Inlined.

Example

iex> Matrex.fill(3, 55)
#Matrex[3×3]
┌                         ┐
│    33.0    33.0    33.0 │
│    33.0    33.0    33.0 │
│    33.0    33.0    33.0 │
└                         ┘

fill(rows, cols, value)

fill(index(), index(), element()) :: matrex()

Create matrix filled with given value. NIF.

Example

iex> Matrex.fill(4,3, 55)
#Matrex[4×3]
┌                         ┐
│    55.0    55.0    55.0 │
│    55.0    55.0    55.0 │
│    55.0    55.0    55.0 │
│    55.0    55.0    55.0 │
└                         ┘

find(matrex, value)

find(matrex(), element()) :: {index(), index()} | nil

Find position of the first occurence of the given value in the matrix. NIF.

Returns {row, column} tuple or nil, if nothing was found. One-based.

Example

first(arg)

first(matrex()) :: element()

Return first element of a matrix.

Example

iex> Matrex.new([[6,5,4],[3,2,1]]) |> Matrex.first()
6.0

forward_substitute(arg1, arg2)

forward_substitute(matrex(), matrex()) :: matrex()

Matrix forward substitution. NIF, via naive C implementation.

The first matrix must be square while the number of columns of the first matrix must equal the number of rows of the second.

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.forward_substitute(
...>   Matrex.new([[3, 4], [4, 8]]) |> Matrex.cholesky(),
...>   Matrex.new([[1],[2]]))
#Matrex[2×1]
┌         ┐
│ 0.57735 │
│ 0.40825 │
└         ┘

get(matrex, key, default)

heatmap(matrex, type \\ :mono256, opts \\ [])

heatmap(
  matrex(),
  :mono8 | :color8 | :mono256 | :color256 | :mono24bit | :color24bit,
  keyword()
) :: matrex()

Prints monochrome or color heatmap of the matrix to the console.

Supports 8, 256 and 16mln of colors terminals. Monochrome on 256 color palette is the default.

type can be :mono8, :color8, :mono256, :color256, :mono24bit and :color24bit.

Special float values, like infinity and not-a-number are marked with contrast colors on the map.

Options

:at — positions heatmap at the specified {row, col} position inside terminal.
:title — sets the title of the heatmap.

Examples

identity(size)

identity(index()) :: matrex()

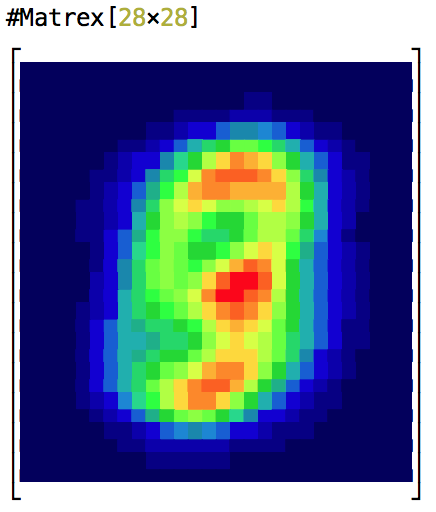
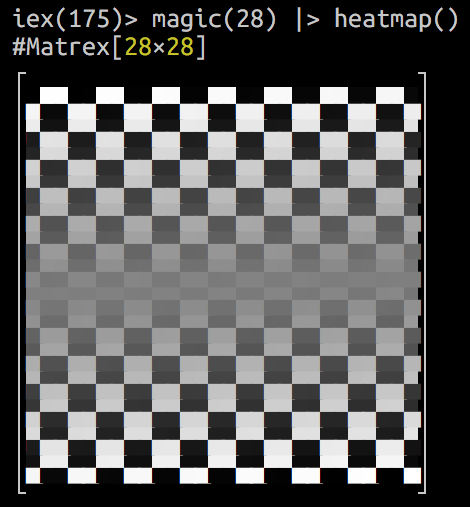
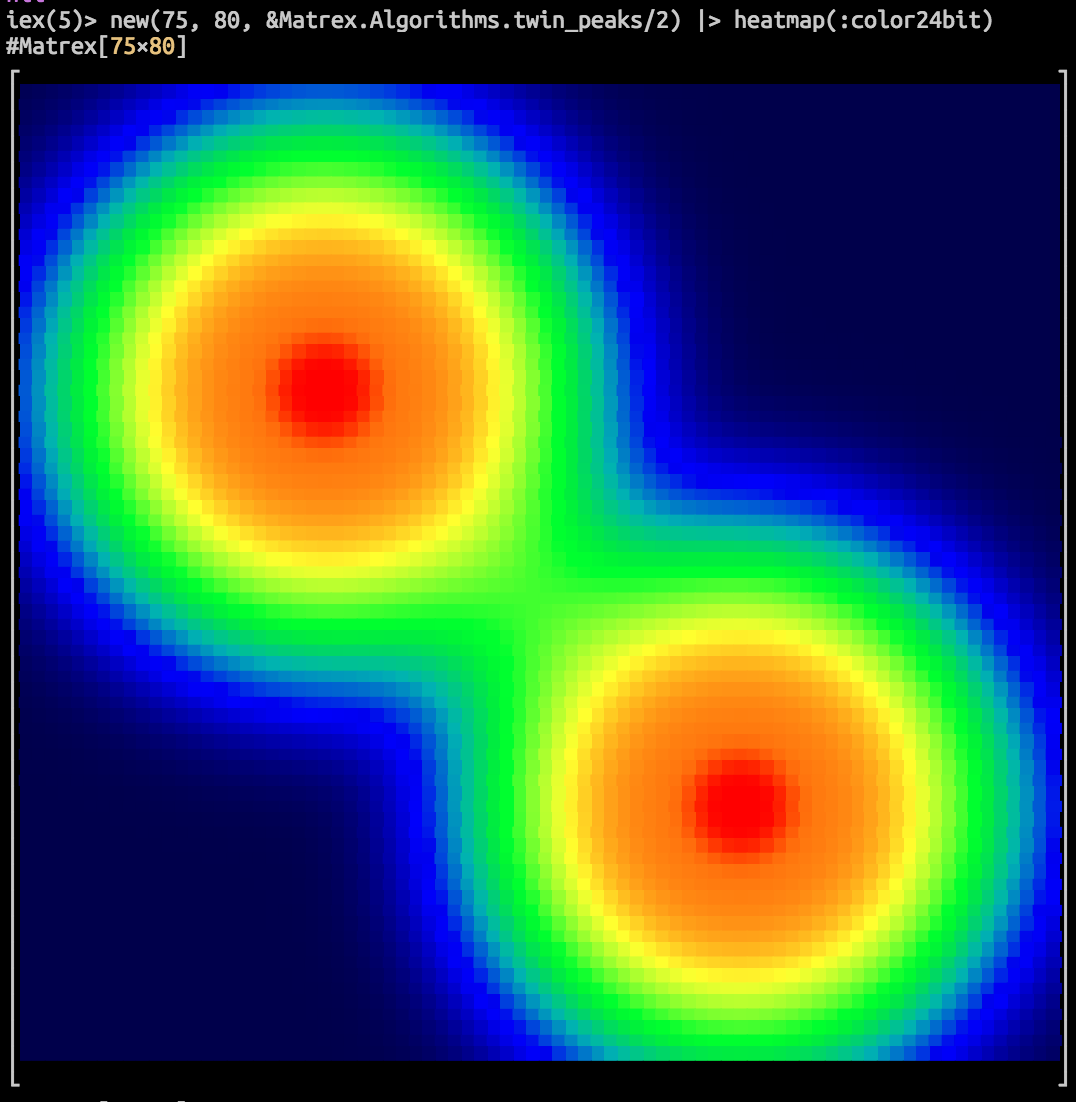
An alias for eye/1.

list_of_rows(arg)

list_of_rows(matrex()) :: [matrex()]

Returns list of all rows of a matrix as single-row matrices.

Example

iex> m = Matrex.reshape(1..6, 3, 2)
#Matrex[6×2]
┌                 ┐
│     1.0     2.0 │
│     3.0     4.0 │
│     5.0     6.0 │
└                 ┘
iex> Matrex.list_of_rows(m)
[#Matrex[1×2]
┌                 ┐
│     1.0     2.0 │
└                 ┘,
#Matrex[1×2]
┌                 ┐
│     3.0     4.0 │
└                 ┘,
#Matrex[1×2]
┌                 ┐
│     5.0     6.0 │
└                 ┘]

list_of_rows(arg1, arg2)

list_of_rows(matrex(), Range.t()) :: [matrex()]

Returns range of rows of a matrix as list of 1-row matrices.

Example

iex> m = Matrex.reshape(1..12, 6, 2)
#Matrex[6×2]
┌                 ┐
│     1.0     2.0 │
│     3.0     4.0 │
│     5.0     6.0 │
│     7.0     8.0 │
│     9.0    10.0 │
│    11.0    12.0 │
└                 ┘
iex> Matrex.list_of_rows(m, 2..4)
[#Matrex[1×2]
┌                 ┐
│     3.0     4.0 │
└                 ┘,
#Matrex[1×2]
┌                 ┐
│     5.0     6.0 │
└                 ┘,
#Matrex[1×2]
┌                 ┐
│     7.0     8.0 │
└                 ┘]

load(file_name)

load(binary()) :: matrex()

Load matrex from file.

.csv and .mtx (binary) formats are supported.

Example

iex> Matrex.load("test/matrex.csv")
#Matrex[5×4]
┌                                 ┐
│     0.0  4.8e-4-0.00517-0.01552 │
│-0.01616-0.01622 -0.0161-0.00574 │
│  6.8e-4     0.0     0.0     0.0 │
│     0.0     0.0     0.0     0.0 │
│     0.0     0.0     0.0     0.0 │
└                                 ┘

load(file_name, format)

load(binary(), :idx | :csv | :mtx) :: matrex()

magic(n)

magic(index()) :: matrex()

Creates "magic" n*n matrix, where sums of all dimensions are equal.

Example

iex> Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘

max(matrex)

max(matrex()) :: element()

Maximum element in a matrix. NIF.

Example

iex> m = Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘
iex> Matrex.max(m)
25.0

iex> Matrex.reshape([1, 2, :inf, 4, 5, 6], 2, 3) |> max()
:inf

max_finite(matrex)

max_finite(matrex()) :: float()

Returns maximum finite element of a matrex. NIF.

Used on matrices which may contain infinite values.

Example

iex>Matrex.reshape([1, 2, :inf, 3, :nan, 5], 3, 2) |> Matrex.max_finite()
5.0

min(matrex)

min(matrex()) :: element()

Minimum element in a matrix. NIF.

Example

iex> m = Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘
iex> Matrex.min(m)
1.0

iex> Matrex.reshape([1, 2, :neg_inf, 4, 5, 6], 2, 3) |> max()
:neg_inf

min_finite(matrex)

min_finite(matrex()) :: float()

Returns minimum finite element of a matrex. NIF.

Used on matrices which may contain infinite values.

Example

iex>Matrex.reshape([1, 2, :neg_inf, 3, 4, 5], 3, 2) |> Matrex.min_finite()
1.0

multiply(scalar, scalar)

multiply(matrex(), matrex()) :: matrex()

multiply(matrex(), number()) :: matrex()

multiply(number(), matrex()) :: matrex()

Elementwise multiplication of two matrices or matrix and a scalar. NIF.

Raises ErlangError if matrices' sizes do not match.

Examples

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.multiply(Matrex.new([[5, 2, 1], [3, 4, 6]]))
#Matrex[2×3]
┌                         ┐
│     5.0     4.0     3.0 │
│    12.0    20.0    36.0 │
└                         ┘

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |> Matrex.multiply(2)
#Matrex[2×3]
┌                         ┐
│     2.0     4.0     6.0 │
│     8.0    10.0    12.0 │
└                         ┘

neg(matrex)

neg(matrex()) :: matrex()

Negates each element of the matrix. NIF.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |> Matrex.neg()
#Matrex[2×3]
┌                         ┐
│    -1.0    -2.0    -3.0 │
│    -4.0    -5.0    -6.0 │
└                         ┘

new(lol_of_ma)

new([[element()]] | [[matrex()]] | binary()) :: matrex()

Creates new matrix from list of lists or text representation (compatible with MathLab/Octave).

List of lists can contain other matrices, which are concatenated in one.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]])
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘

iex> Matrex.new([[Matrex.fill(2, 1.0), Matrex.fill(2, 3, 2.0)],
...> [Matrex.fill(1, 2, 3.0), Matrex.fill(1, 3, 4.0)]])
#Matrex[5×5]
┌                                         ┐
│     1.0     1.0     2.0     2.0     2.0 │
│     1.0     1.0     2.0     2.0     2.0 │
│     3.0     3.0     4.0     4.0     4.0 │
└                                         ┘

iex> Matrex.new("1;0;1;0;1")
#Matrex[5×1]
┌         ┐
│     1.0 │
│     0.0 │
│     1.0 │
│     0.0 │
│     1.0 │
└         ┘

iex> Matrex.new("""
...>         1.00000   0.10000   0.60000   1.10000
...>         1.00000   0.20000   0.70000   1.20000
...>         1.00000       NaN   0.80000   1.30000
...>             Inf   0.40000   0.90000   1.40000
...>         1.00000   0.50000    NegInf   1.50000
...>       """)
#Matrex[5×4]
┌                                 ┐
│     1.0     0.1     0.6     1.1 │
│     1.0     0.2     0.7     1.2 │
│     1.0    NaN      0.8     1.3 │
│     ∞       0.4     0.9     1.4 │
│     1.0     0.5    -∞       1.5 │
└                                 ┘

new(rows, columns, function)

new(index(), index(), (() -> element())) :: matrex()

new(index(), index(), (index(), index() -> element())) :: matrex()

Creates new matrix with values provided by the given function.

If function accepts two arguments one-based row and column index of each element are passed to it.

Examples

iex> Matrex.new(3, 3, fn -> :rand.uniform() end)
#Matrex[3×3]
┌                         ┐
│ 0.45643 0.91533 0.25332 │
│ 0.29095 0.21241  0.9776 │
│ 0.42451 0.05422 0.92863 │
└                         ┘

iex> Matrex.new(3, 3, fn row, col -> row*col end)
#Matrex[3×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     2.0     4.0     6.0 │
│     3.0     6.0     9.0 │
└                         ┘

normalize(matrex)

normalize(matrex()) :: matrex()

Bring all values of matrix into [0, 1] range. NIF.

Where 0 corresponds to the minimum value of the matrix, and 1 — to the maxixmim.

Example

iex> m = Matrex.reshape(1..9, 3, 3)
#Matrex[3×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
│     7.0     8.0     9.0 │
└                         ┘
iex> Matrex.normalize(m)
#Matrex[3×3]
┌                         ┐
│     0.0   0.125    0.25 │
│   0.375     0.5   0.625 │
│    0.75   0.875     1.0 │
└                         ┘

ones(size)

ones(index()) :: matrex()

ones({index(), index()}) :: matrex()

Create matrex of ones of square dimensions or consuming output of size/1 function.

Examples

iex> Matrex.ones(3)
#Matrex[3×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
└                         ┘

iex> m = Matrex.new("1 2 3; 4 5 6")
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘
iex> Matrex.ones(Matrex.size(m))
#Matrex[2×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
└                         ┘

ones(rows, cols)

ones(index(), index()) :: matrex()

Create matrix filled with ones.

Example

iex> Matrex.ones(2, 3)
#Matrex[2×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
└                         ┘

print(matrex, opts \\ [rows: 21])

print(matrex(), Keyword.t()) :: matrex()

Prints matrix to the console.

Accepted options:

:rows — number of rows of matrix to show. Defaults to 21
:columns — number of columns of matrix to show. Defaults to maximum number of column, that fits into current terminal width.

Returns the matrix itself, so can be used in pipes.

Example

iex> print(m, rows: 5, columns: 3) #Matrex[20×20] ┌ ┐ │ 1.0 399.0 … 20.0 │ │ 380.0 22.0 … 361.0 │ │ 360.0 42.0 … 341.0 │ │ ⋮ ⋮ … ⋮ │ │ 40.0 362.0 … 21.0 │ │ 381.0 19.0 … 400.0 │ └ ┘

random(size)

random(index()) :: matrex()

Create square matrix of random floats.

See random/2 for details.

Example

iex> Matrex.random(3)
#Matrex[3×3]
┌                         ┐
│ 0.66438 0.31026 0.98602 │
│ 0.82127 0.04701 0.13278 │
│ 0.96935 0.70772 0.98738 │
└                         ┘

random(rows, columns)

random(index(), index()) :: matrex()

Create matrix of random floats in [0, 1] range. NIF.

C language RNG is seeded on NIF libray load with srandom(time(NULL) + clock()).

Example

iex> Matrex.random(4,3)
#Matrex[4×3]
┌                         ┐
│ 0.32994 0.28736 0.88012 │
│ 0.51782 0.68608 0.29976 │
│ 0.52953  0.9071 0.26743 │
│ 0.82189 0.59311  0.8451 │
└                         ┘

reshape(enum, rows, columns)

reshape([matrex()], index(), index()) :: matrex()

reshape([element()], index(), index()) :: matrex()

reshape(matrex(), index(), index()) :: matrex()

reshape(Range.t(), index(), index()) :: matrex()

reshape(Enumerable.t(), index(), index()) :: matrex()

Reshapes list of values into a matrix of given size or changes the shape of existing matrix.

Takes a list or anything, that implements Enumerable.to_list/1.

Can take a list of matrices and concatenate them into one big matrix.

Raises ArgumentError if list size and given shape do not match.

Example

iex> [1, 2, 3, 4, 5, 6] |> Matrex.reshape(2, 3)
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘

iex> Matrex.reshape([Matrex.zeros(2), Matrex.ones(2),
...> Matrex.fill(3, 2, 2.0), Matrex.fill(3, 2, 3.0)], 2, 2)
#Matrex[5×4]
┌                                 ┐
│     0.0     0.0     1.0     1.0 │
│     0.0     0.0     1.0     1.0 │
│     2.0     2.0     3.0     3.0 │
│     2.0     2.0     3.0     3.0 │
│     2.0     2.0     3.0     3.0 │
└                                 ┘

iex> Matrex.reshape(1..6, 2, 3)
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘

iex> Matrex.new("1 2 3; 4 5 6") |> Matrex.reshape(3, 2)
#Matrex[3×2]
┌                 ┐
│     1.0     2.0 │
│     3.0     4.0 │
│     5.0     6.0 │
└                 ┘

resize(matrex, scale, method \\ :nearest)

resize(matrex(), number(), :nearest | :bilinear) :: matrex()

Resize matrix by scaling its dimenson with scale. NIF.

Examples

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex(3)> Matrex.resize(m, 2)
#Matrex[6×6]
┌                                                 ┐
│     8.0     8.0     1.0     1.0     6.0     6.0 │
│     8.0     8.0     1.0     1.0     6.0     6.0 │
│     3.0     3.0     5.0     5.0     7.0     7.0 │
│     3.0     3.0     5.0     5.0     7.0     7.0 │
│     4.0     4.0     9.0     9.0     2.0     2.0 │
│     4.0     4.0     9.0     9.0     2.0     2.0 │
└                                                 ┘

iex(4)> m = Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘
iex(5)> Matrex.resize(m, 0.5)
#Matrex[3×3]
┌                         ┐
│    16.0    23.0     7.0 │
│    22.0     4.0    13.0 │
│     9.0    11.0    25.0 │
└                         ┘

row(arg, row)

row(matrex(), index()) :: matrex()

Get row of matrix as matrix (vector) in matrex form. One-based.

You can use shorter matrex[n] syntax for the same result.

Example

iex> m = Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘
iex> Matrex.row(m, 4)
#Matrex[1×5]
┌                                         ┐
│     9.0    11.0    18.0    25.0     2.0 │
└                                         ┘
iex> m[4]
#Matrex[1×5]
┌                                         ┐
│     9.0    11.0    18.0    25.0     2.0 │
└                                         ┘

row_to_list(matrex, row)

row_to_list(matrex(), index()) :: [element()]

Return matrix row as list by one-based index.

Example

iex> m = Matrex.magic(5)
#Matrex[5×5]
┌                                         ┐
│    16.0    23.0     5.0     7.0    14.0 │
│    22.0     4.0     6.0    13.0    20.0 │
│     3.0    10.0    12.0    19.0    21.0 │
│     9.0    11.0    18.0    25.0     2.0 │
│    15.0    17.0    24.0     1.0     8.0 │
└                                         ┘
iex> Matrex.row_to_list(m, 3)
[3.0, 10.0, 12.0, 19.0, 21.0]

save(matrex, file_name)

save(matrex(), binary()) :: :ok | :error

Saves matrex into file.

Binary (.mtx) and CSV formats are supported currently.

Format is defined by the extension of the filename.

Example

iex> Matrex.random(5) |> Matrex.save("r.mtx")
:ok

scalar(matrex)

scalar(matrex()) :: element()

Transfer one-element matrix to a scalar value.

Differently from first/1 will not match and throw an error, if matrix contains more than one element.

Example

iex> Matrex.new([[1.234]]) |> Matrex.scalar()
1.234

iex> Matrex.new([[0]]) |> Matrex.divide(0) |> Matrex.scalar()
:nan

iex> Matrex.new([[1.234, 5.678]]) |> Matrex.scalar()
** (FunctionClauseError) no function clause matching in Matrex.scalar/1

set(arg, row, column, value)

set(matrex(), index(), index(), element()) :: matrex()

Set element of matrix at the specified position (one-based) to new value.

Example

iex> m = Matrex.ones(3)
#Matrex[3×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
│     1.0     1.0     1.0 │
└                         ┘
iex> m = Matrex.set(m, 2, 2, 0)
#Matrex[3×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     0.0     1.0 │
│     1.0     1.0     1.0 │
└                         ┘
iex> m = Matrex.set(m, 3, 2, :neg_inf)
#Matrex[3×3]
┌                         ┐
│     1.0     1.0     1.0 │
│     1.0     0.0     1.0 │
│     1.0     -∞      1.0 │
└                         ┘

set_column(arg1, column, arg2)

set_column(matrex(), index(), matrex()) :: matrex()

Set column of a matrix to the values from the given 1-column matrix. NIF.

Example

iex> m = Matrex.reshape(1..6, 3, 2)
#Matrex[3×2]
┌                    ┐
│     1.0     2.0    │
│     3.0     4.0    │
│     5.0     6.0    │
└                    ┘

iex> Matrex.set_column(m, 2, Matrex.new("7; 8; 9"))
#Matrex[3×2]
┌                    ┐
│     1.0     7.0    │
│     3.0     8.0    │
│     5.0     9.0    │
└                    ┘

size(arg)

size(matrex()) :: {index(), index()}

Return size of matrix as {rows, cols}

Example

iex> m = Matrex.random(2,3)
#Matrex[2×3]
┌                         ┐
│ 0.69745 0.23668 0.36376 │
│ 0.63423 0.29651 0.22844 │
└                         ┘
iex> Matrex.size(m)
{2, 3}

square(matrex)

square(matrex()) :: matrex()

Produces element-wise squared matrix. NIF through multiply/4.

Example

iex> m = Matrex.new("1 2 3; 4 5 6")
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘
iex> Matrex.square(m)
#Matrex[2×3]
┌                         ┐
│     1.0     4.0     9.0 │
│    16.0    25.0    36.0 │
└                         ┘

submatrix(matrex, rows, cols)

submatrix(matrex(), Range.t(), Range.t()) :: matrex()

Returns submatrix for a given matrix. NIF.

Rows and columns ranges are inclusive and one-based.

Example

iex> m = Matrex.new("1 2 3; 4 5 6; 7 8 9")
#Matrex[3×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
│     7.0     8.0     9.0 │
└                         ┘
iex> Matrex.submatrix(m, 2..3, 2..3)
#Matrex[2×2]
┌                ┐
│    5.0     6.0 │
│    8.0     9.0 │
└                ┘

subtract(scalar, scalar)

subtract(matrex() | number(), matrex() | number()) :: matrex()

Subtracts two matrices or matrix from scalar element-wise. NIF.

Raises ErlangError if matrices' sizes do not match.

Examples

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.subtract(Matrex.new([[5, 2, 1], [3, 4, 6]]))
#Matrex[2×3]
┌                         ┐
│    -4.0     0.0     2.0 │
│     1.0     1.0     0.0 │
└                         ┘

iex> Matrex.subtract(1, Matrex.new([[1, 2, 3], [4, 5, 6]]))
#Matrex[2×3]
┌                         ┐
│     0.0     -1.0   -2.0 │
│    -3.0    -4.0    -5.0 │
└                         ┘

subtract_inverse(first, second)

subtract_inverse(matrex() | number(), matrex() | number()) :: matrex()

Subtracts the second matrix or scalar from the first. Inlined.

Raises ErlangError if matrices' sizes do not match.

Example

iex> Matrex.new([[1, 2, 3], [4, 5, 6]]) |>
...> Matrex.subtract_inverse(Matrex.new([[5, 2, 1], [3, 4, 6]]))
#Matrex[2×3]
┌                         ┐
│     4.0     0.0    -2.0 │
│    -1.0    -1.0     0.0 │
└                         ┘

iex> Matrex.eye(3) |> Matrex.subtract_inverse(1)
#Matrex[3×3]
┌                         ┐
│     0.0     1.0     1.0 │
│     1.0     0.0     1.0 │
│     1.0     1.0     0.0 │
└                         ┘

sum(matrex)

sum(matrex()) :: element()

Sums all elements. NIF.

Can return special float values as atoms.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.sum(m)
45.0

iex> m = Matrex.new("1 Inf; 2 3")
#Matrex[2×2]
┌                 ┐
│     1.0     ∞   │
│     2.0     3.0 │
└                 ┘
iex> sum(m)
:inf

to_column(m)

to_column(matrex()) :: matrex()

Convert any matrix m×n to a column matrix (m*n)×1.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.to_column(m)
#Matrex[1×9]
┌                                                                         ┐
│     8.0     1.0     6.0     3.0     5.0     7.0     4.0     9.0     2.0 │
└                                                                         ┘

to_list(matrex)

to_list(matrex()) :: [element()]

Converts to flat list. NIF.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.to_list(m)
[8.0, 1.0, 6.0, 3.0, 5.0, 7.0, 4.0, 9.0, 2.0]

to_list_of_lists(matrex)

to_list_of_lists(matrex()) :: [[element()]]

Converts to list of lists. NIF.

Examples

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.to_list_of_lists(m)
[[8.0, 1.0, 6.0], [3.0, 5.0, 7.0], [4.0, 9.0, 2.0]]

iex> r = Matrex.divide(Matrex.eye(3), Matrex.zeros(3))
#Matrex[3×3]
┌                         ┐
│     ∞      NaN     NaN  │
│    NaN      ∞      NaN  │
│    NaN     NaN      ∞   │
└                         ┘
iex> Matrex.to_list_of_lists(r)
[[:inf, :nan, :nan], [:nan, :inf, :nan], [:nan, :nan, :inf]]

to_row(m)

to_row(matrex()) :: matrex()

Convert any matrix m×n to a row matrix 1×(m*n).

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.to_row(m)
#Matrex[1×9]
┌                                                                         ┐
│     8.0     1.0     6.0     3.0     5.0     7.0     4.0     9.0     2.0 │
└                                                                         ┘

trace(matrex)

trace(matrex()) :: element()

Trace of matrix (sum of all diagonal elements). Elixir.

Can return special float values as atoms.

Example

iex> m = Matrex.magic(3)
#Matrex[3×3]
┌                         ┐
│     8.0     1.0     6.0 │
│     3.0     5.0     7.0 │
│     4.0     9.0     2.0 │
└                         ┘
iex> Matrex.trace(m)
15.0

iex> m = Matrex.new("Inf 1; 2 3")
#Matrex[2×2]
┌                 ┐
│     ∞       1.0 │
│     2.0     3.0 │
└                 ┘
iex> trace(m)
:inf

transpose(m)

transpose(matrex()) :: matrex()

Transposes a matrix. NIF.

Example

iex> m = Matrex.new([[1,2,3],[4,5,6]])
#Matrex[2×3]
┌                         ┐
│     1.0     2.0     3.0 │
│     4.0     5.0     6.0 │
└                         ┘
iex> Matrex.transpose(m)
#Matrex[3×2]
┌                 ┐
│     1.0     4.0 │
│     2.0     5.0 │
│     3.0     6.0 │
└                 ┘

update(arg, row, col, fun)

update(matrex(), index(), index(), (element() -> element())) :: matrex()

Updates the element at the given position in matrix with function.

Function is invoked with the current element value

Example

iex> m = Matrex.reshape(1..6, 3, 2)
#Matrex[3×2]
┌                 ┐
│     1.0     2.0 │
│     3.0     4.0 │
│     5.0     6.0 │
└                 ┘
iex> Matrex.update(m, 2, 2, fn x -> x * x end)
#Matrex[3×2]
┌                 ┐
│     1.0     2.0 │
│     3.0    16.0 │
│     5.0     6.0 │
└                 ┘

zeros(size)

zeros(index() | {index(), index()}) :: matrex()

Create square matrix of size size rows × size columns, filled with zeros. Inlined.

Example

iex> Matrex.zeros(3)
#Matrex[3×3]
┌                         ┐
│     0.0     0.0     0.0 │
│     0.0     0.0     0.0 │
│     0.0     0.0     0.0 │
└                         ┘

zeros(rows, cols)

zeros(index(), index()) :: matrex()

Create matrix of zeros of the specified size. NIF, using memset().

Faster, than fill(rows, cols, 0).

Example

iex> Matrex.zeros(4,3)
#Matrex[4×3]
┌                         ┐
│     0.0     0.0     0.0 │
│     0.0     0.0     0.0 │
│     0.0     0.0     0.0 │
│     0.0     0.0     0.0 │
└                         ┘