Scurry.Polygon (Scurry v3.0.1)

View Source

Functions related to polygons and lines relevant for 2D map pathfinding.

This provides functions for;

  • line of sight between two points
  • classify polygon vertices as concave or vertex
  • intersections of lines and polygons
  • checking if points are inside/outside polygons
  • finding nearest point on a polygon and distances

Polygons are

  • A list of vertices, [{x1, y1}, {x2,y2}, ...] defined as a list(vector).
  • They must not be closed, ie. last vertex should not be equal to the first.
  • They must be in clockwise order in screen coordinates, otherwise convex/concave classification will be inversed as it traverses the egdes.

Order of vertices

Polygons must be defined in clockwise order in screen coordinates. This is necessary for the convex/concave classification. It counter clock, it will be inversed as it traverses the egdes.

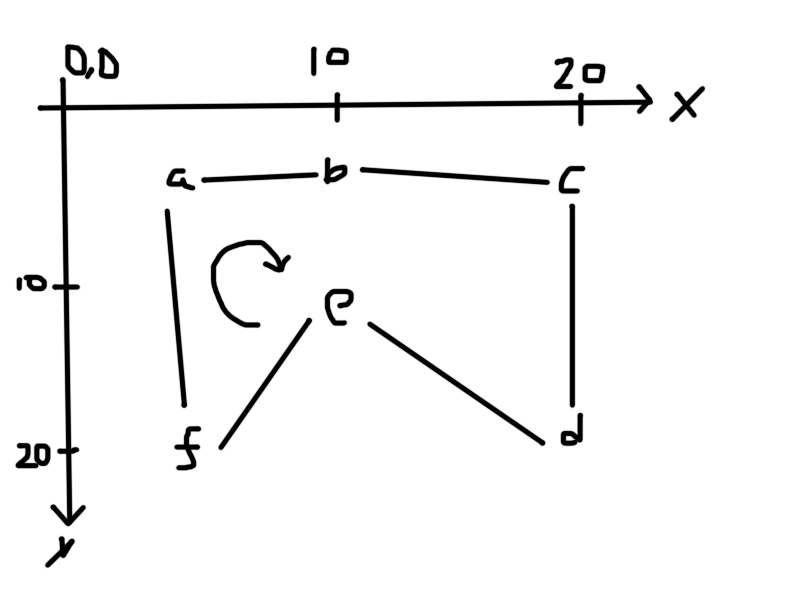
Here's a crude drawing of an example of the M shaped polygon used for many tests/docs.

polygon = [{0, 0}, {10, 0}, {20, 0}, {20, 20}, {10, 10}, {0, 20}] Order of vertices

Summary

Types

line()

A line is represented by two vertices of type vector/0

polygon()

A polygon is represented by a list of vector/0, each being a tuple of {x, y} coordinates, both number/0. To be properly defined, the vertices of the polygon must be non-closed and clockwise.

vector()

A vector is represented as a tuple {x, y}, it's x and y components, both number/0. These are used for vector math in Scurry.Vector and as 2D points in Scurry.Polygon and Scurry.PolygonMap.

Functions

classify_vertex(polygon, at)

Check if a specific vertex is concave, convex or neither.

classify_vertices(polygon)

Split a polygon into concave and convex vertices.

first_intersection(polygon, line)

Get first intersection of a line with a polygon.

intersections(polygon, line, opts \\ [])

Get all intersections of a line with a polygon including their type.

intersects(polygon, line)

Checks if a line intersects a polygon.

intersects?(polygon, line)

Checks if a line intersects a polygon.

is_clockwise?(polygon)

Check if the polygon is clockwise within screen coordinates.

is_concave?(polygon, at)

Check if a specific vertex in a polygon is concave

is_convex?(polygon, at)

Check if a specific vertex in a polygon is convex

is_inside?(polygon, point, opts \\ [])

Check if a point is inside a polygon or not.

is_outside?(polygon, point, opts \\ [])

The opposite of is_inside?/3, provided for code readability.

last_intersection(polygon, line)

Get last intersection of a line with a polygon.

nearest_edge(polygon, point)

Find the edge of a polygon nearest a given point.

nearest_point_on_edge(polygon, point)

Find the point on the edge of a polygon nearest a given point.

Types

line()

@type line() :: {vector(), vector()}

A line is represented by two vertices of type vector/0

polygon()

@type polygon() :: [vector()]

A polygon is represented by a list of vector/0, each being a tuple of {x, y} coordinates, both number/0. To be properly defined, the vertices of the polygon must be non-closed and clockwise.

vector()

@type vector() :: {x :: number(), y :: number()}

A vector is represented as a tuple {x, y}, it's x and y components, both number/0. These are used for vector math in Scurry.Vector and as 2D points in Scurry.Polygon and Scurry.PolygonMap.

Functions

classify_vertex(polygon, at)

@spec classify_vertex(polygon(), integer()) :: :concave | :convex | :neither

Check if a specific vertex is concave, convex or neither.

Whehter a vertex is concave or convex is defined by it pointing out - it's inner angle is less than 180 means convex and more than 180 means concave.

When testing a vertex, keep this in mind and negate appropriately depending on whether it's the boundary polygon or a hole polygon being tested.

Params

  • polygon (polygon/0) the polygon in which to check a vertex.
  • at (integer/0), which vertex in the polygon to check.

Returns

  • :convex for a convex vertice.
  • :concave for a concave vertice.
  • :neither for a vertice that's a straight edge, ie. 180 degrees.

Examples 

# A vaguely M shaped polygon
iex> m = [{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
[{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
iex> Polygon.classify_vertex(m, 0)
:convex
iex> Polygon.classify_vertex(m, 1)
:neither
iex> Polygon.classify_vertex(m, 4)
:concave

classify_vertices(polygon)

@spec classify_vertices(polygon()) :: {[vector()], [vector()]}

Split a polygon into concave and convex vertices.

When doing pathfinding, there will typically be a outer polygon bounding the "world" and multiple inner polygons describing "holes/obstacles".

The path can only be within the outer polygon and has to "walk around" the holes.

Classifying the polygons into concave and convex is used to determine the walkable graph.

  • The outer polygon's concave (pointing into the world) vertices are used. used.
  • The holes' convex (point out of the hole, into the world) vertices used used.

In code, this looks like

# Get the concave vectices of the bounding polygon
{concave, _convex} = Polygon.classify_vertices(world)

# Get al lthe convex vertices of all the holes
convex = Enum.reduce(holes, [], fn points, acc ->
  {_, convex} = Polygon.classify_vertices(points)
  acc ++ convex
end)

# The initial walk map is the combined set
vertices = concave ++ convex

Params

Returns

{list of concave vertices, list of convex}.

  • A tuple of two lists of vector/0.
  • The first list are all the concave vertices or [] if none
  • The second list are all the convex vertices or [] if none

Note

Three points that fall on the same line ([{0, 0}, {1, 0}, {2, 0}]) does not match neither the concave/convex definition (angle greater-than / less-than 180 degrees) this function will discard these via classify_vertex/2.

Examples 

# A vaguely M shaped polygon
iex> Polygon.classify_vertices([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}])
{[{1, 0.5}], [{0, 0}, {2, 0}, {2, 1}, {0, 1}]}

# A square around 0,0
iex> Polygon.classify_vertices([{-1, -1}, {1, -1}, {1, 1}, {-1, 1}])
{[], [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]}

# A flat line
iex> Polygon.classify_vertices([{0, 0}, {1, 0}, {2, 0}])
{[], []}

first_intersection(polygon, line)

@spec first_intersection(polygon(), line()) :: nil | vector()

Get first intersection of a line with a polygon.

The "opposite" of last_intersection/2.

Params

  • polygon (polygon/0) a polygon to check for an intersection with line.
  • line (line/0). The line to check for intersections with polygon.

A line/0 is a tuple of two vector/0 and the first is considered the head of the line and "first" in this context means nearest to that point.

Returns

  • A vector/0 indicating where line first intersects polygon.
  • nil if there's no intersection.

Examples 

# A square around 0,0
iex> square = [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
[{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
iex> Polygon.first_intersection(square, {{0, -2}, {0, 2}})
{0.0, -1.0}
iex> Polygon.first_intersection(square, {{0, 2}, {0, -2}})
{0.0, 1.0}
iex> Polygon.first_intersection(square, {{2, -2}, {2, 2}})
nil

intersections(polygon, line, opts \\ [])

@spec intersections(polygon(), line(), [{:allow_points, boolean()}]) :: [vector()]

Get all intersections of a line with a polygon including their type.

This function basically calls Geo.line_segment_intersection/2 for every segment of the polygon against the line and filters the results to only include the list of intersection points.

Params

  • polygon (polygon/0), the polygon to check.
  • line (line/0), the line check for intersections against polygon.

Options

  • :allow_points (default false) whether a on_point intersection should be considered an intersection or not. This varies from use cases. Eg. when building a polygon, points will be connected and thus intersect if true. This may not be the desired result, so false won't consider points intersections.

Returns

  • a list of vector/0 indicating where the line intersects
  • [] if there's no intersections.

Examples 

iex> polygon = [{0, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
[{0, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
iex> line = {{1, -1}, {1, 3}}
{{1, -1}, {1, 3}}
iex> Polygon.intersections(polygon, line)
[{1.0, 0.0}]
iex> Polygon.intersections(polygon, line, allow_points: true)
[{1.0, 0.0}, {1.0, 0.5}]

intersects(polygon, line)

@spec intersects(polygon(), line()) ::
  :nointersection
  | :on_segment
  | {:intersection, vector()}
  | {:poiont_intersection, vector()}

Checks if a line intersects a polygon.

Find an intersection (if any) between polygon and line. For most cases using intersections/3 will be a better choice to get intersections.

Params

  • polygon (polygon/0), the polygon to check.
  • line (line/0), the line to check if it intersects polygon.

Returns

This relates to Scurry.Geo.line_segment_intersection/2.

  • :nointersection, line does not intersect polygon
  • {:point_intersection, vector}
  • {;intersection, line}
  • :on_segment

Examples 

# A vaguely M shaped polygon
iex> Polygon.intersects([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{1, -0.5}, {1, 0.5}})
{:point_intersection, {1.0, 0.0}}
iex> Polygon.intersects([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{0.5, -0.5}, {0.5, 0.5}})
{:intersection, {0.5, 0.0}}
iex> Polygon.intersects([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{0.5, -1}, {0.5, 0}})
{:point_intersection, {0.5, 0.0}}
iex> Polygon.intersects([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{0.5, -2}, {0.5, -1}})
:nointersection
iex> Polygon.intersects([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{2, 0.1}, {2, 0.9}})
:on_segment

intersects?(polygon, line)

@spec intersects?(polygon(), line()) :: boolean()

Checks if a line intersects a polygon.

This is a boolean version of intersects/2. For most cases using intersections/3 will be a better choice to get intersections.

Params

  • polygon (polygon/0), the polygon to check.
  • line (line/0), the line to check if it intersects polygon.

Returns

true or false wether the line intersects the polygon or not.

Examples 

# A vaguely M shaped polygon
iex> Polygon.intersects?([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{1, -0.5}, {1, 0.5}})
true
iex> Polygon.intersects?([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{1, -1}, {1, 0}})
true
iex> Polygon.intersects?([{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}], {{1, -2}, {1, -1}})
false

is_clockwise?(polygon)

@spec is_clockwise?(polygon()) :: boolean()

Check if the polygon is clockwise within screen coordinates.

This is provided as a utility to check polygons eg. if loading them from data files. The library internally does not use this to validate polygons to avoid a runtime penalty.

Params

  • polygon (polygon/0) the polygon to check to check.

Returrns

true if the points in the polygon are defined in a clockwise orientation.

Examples 

iex> Polygon.is_clockwise?([{0, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}])
true
iex> Polygon.is_clockwise?([{0, 0}, {0, 1}, {1, 0.5}, {2, 1}, {2, 0}])
false

is_concave?(polygon, at)

@spec is_concave?(polygon(), number()) :: boolean()

Check if a specific vertex in a polygon is concave

Params

  • polygon (polygon/0) the polygon in which to check a vertex.
  • at (integer/0), which vertex in the polygon to check.

Returns

true if the vertex is concave, otherwise false

See also classify_vertex/2.

Examples 

# A vaguely M shaped polygon
iex> m = [{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
[{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
iex> Polygon.is_concave?(m, 0)
false
iex> Polygon.is_concave?(m, 1)
false
iex> Polygon.is_concave?(m, 2)
false
iex> Polygon.is_concave?(m, 3)
false
iex> Polygon.is_concave?(m, 4)
true
iex> Polygon.is_concave?(m, 5)
false

is_convex?(polygon, at)

@spec is_convex?(polygon(), number()) :: boolean()

Check if a specific vertex in a polygon is convex

Params

  • polygon (polygon/0) the polygon in which to check a vertex.
  • at (integer/0), which vertex in the polygon to check.

Returns

true if the vertex is convex, otherwise false

See also classify_vertex/2.

Examples 

# A vaguely M shaped polygon
iex> m = [{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
[{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 0.5}, {0, 1}]
iex> Polygon.is_convex?(m, 0)
true
iex> Polygon.is_convex?(m, 1)
false
iex> Polygon.is_convex?(m, 2)
true
iex> Polygon.is_convex?(m, 3)
true
iex> Polygon.is_convex?(m, 4)
false
iex> Polygon.is_convex?(m, 5)
true

is_inside?(polygon, point, opts \\ [])

@spec is_inside?(polygon(), vector(), [{:allow_border, boolean()}]) :: boolean()

Check if a point is inside a polygon or not.

Params

  • polygon (polygon/0) the polygon to check against.
  • point (vector/0) the point to check if is inside (or on) polygon.

Options

  • allow_border, defaults to true and allows point to be the polygon edges.

Returns

  • true is the point is inside the polygon
  • true is the point is on polygon edges if allow_border is true.

Examples 

# A square around 0,0
iex> square = [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
[{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
iex> Polygon.is_inside?(square, {0, 0})
true
iex> Polygon.is_inside?(square, {-1, 0})
true
iex> Polygon.is_inside?(square, {-1, 0}, [allow_border: false])
false
iex> Polygon.is_inside?(square, {-2, 0})
false

is_outside?(polygon, point, opts \\ [])

The opposite of is_inside?/3, provided for code readability.

See is_inside?/3 for behaviour and imagine the opposite.

last_intersection(polygon, line)

@spec last_intersection(polygon(), line()) :: nil | vector()

Get last intersection of a line with a polygon.

The "opposite" of first_intersection/2.

Params

  • polygon (polygon/0) a polygon to check for an intersection with line.
  • line (line/0). The line to check for intersections with polygon.

A line/0 is a tuple of two vector/0 and the last is considered the tail of the line and "last" in this context means nearest to that point.

Returns

  • A vector/0 indicating where line last intersects polygon
  • nil if there's no intersection.

Examples 

# A square around 0,0
iex> square = [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
[{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
iex> Polygon.last_intersection(square, {{0, -2}, {0, 2}})
{0.0, 1.0}
iex> Polygon.last_intersection(square, {{0, 2}, {0, -2}})
{0.0, -1.0}
iex> Polygon.last_intersection(square, {{2, -2}, {2, 2}})
nil

nearest_edge(polygon, point)

@spec nearest_edge(polygon(), vector()) :: line()

Find the edge of a polygon nearest a given point.

Given a point that's inside or outside a given polygon, this checks each segment of the polygon, and returns the nearest one.

If multiple lines are "nearest", the first in the polygon is picked.

Params

  • polygon (polygon/0) the polygion to find the nearest edge on.
  • point (vector/0) the point to find the nearest edge to.

Returns

A line/0 that is a segment of polygon that is closest to point.

Examples 

# A square around 0,0
iex> square = [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
[{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
iex> Polygon.nearest_edge(square, {0, 0})
{{-1, -1}, {1, -1}}
iex> Polygon.nearest_edge(square, {0.9, 0})
{{1, -1}, {1, 1}}
iex> Polygon.nearest_edge(square, {1.1, 0})
{{1, -1}, {1, 1}}

nearest_point_on_edge(polygon, point)

@spec nearest_point_on_edge(polygon(), vector()) :: vector()

Find the point on the edge of a polygon nearest a given point.

Given a point that's inside or outside a given polygon, this uses nearest_edge/2 to find the closest edge and then computes the point on the edge nearest the given point.

Params

  • polygon (polygon/0) the polygion to find the nearest point on.
  • point (vector/0) the point to find the nearest point to.

Returns

A vector/0 that is a point on polygon that is closest to point.

Examples 

# A square around 0,0
iex> square = [{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
[{-1, -1}, {1, -1}, {1, 1}, {-1, 1}]
iex> Polygon.nearest_point_on_edge(square, {0, 0})
{0.0, -1.0}
iex> Polygon.nearest_point_on_edge(square, {0.9, 0})
{1.0, 0.0}
iex> Polygon.nearest_point_on_edge(square, {1.1, 0})
{1.0, 0.0}