View Source k-nearest neighbors (KNN)

Mix.install([
  {:scholar, "~> 0.3.0"},
  {:explorer, "~> 0.8.2", override: true},
  {:exla, "~> 0.7.2"},
  {:nx, "~> 0.7.2"},
  {:req, "~> 0.4.14"},
  {:kino_vega_lite, "~> 0.1.11"},
  {:kino, "~> 0.12.3"},
  {:kino_explorer, "~> 0.1.18"},
  {:tucan, "~> 0.3.1"}
])

Setup

We will use VegaLite, Explorer, and Scholar throughout this guide, so let's define some aliases:

require Explorer.DataFrame, as: DF
require Explorer.Series, as: S
require Explorer.Query, as: Q
alias Scholar.Neighbors.{KNNClassifier, KNNRegressor, BruteKNN}
alias Scholar.Metrics.{Classification, Regression}

And let's configure EXLA as our default backend (where our tensors are stored) and compiler (which compiles Scholar code) across the notebook and all branched sections:

Nx.global_default_backend(EXLA.Backend)
Nx.Defn.global_default_options(compiler: EXLA)
seed = 42
key = Nx.Random.key(42)

#Nx.Tensor<
  u32[2]
  EXLA.Backend<host:0, 0.3809581470.3464101900.76787>
  [0, 42]
>

Use cases

This notebook will cover the three primary applications of k-nearest Neighbors: classification, regression, and anomaly detection. Let's get started with a practical example. Imagine just moved to a new city, and you're here for the first time. Since you're an active person, you'd like to find a nearby gym with good facilities. What would you do? You'd probably start by searching for gyms on online maps. The search results might look something like this:

Now you can check out the gyms and eventually decide which one will be your regular spot. What did the search engine do? It calculated the nearest gyms (nearest neighbors) from your current location, which is the essence of finding nearest neighbors.

Now let's move to a more abstract example. You're listening to your favorite rock playlist and you think, "Yeah, these tracks are cool, but I've been listening to them on repeat. Maybe I should explore some new music." Searching for random songs might not be the most effective approach; you could end up with hip-hop or pop tracks, which you may not enjoy as much. However, it might also lead you to discover entirely new genres. A better approach could be to explore other rock playlists available online. While these playlists align with your preferred genre, they may not consider your unique tastes within rock music. Wouldn't it be great if there were a tool that could recommend new songs based on your previous playlists? Fortunately, such tools exist!

One type of recommendation system relies on collaborative filtering: it recommends songs based on what other users with similar musical tastes (aka its neighbours) listen to. Another approach is to treat songs as points and then compute the closest songs to your favorites. Part of the challenge in solving these problems is how to model users and songs as points in space however, once that is done, KNN algorithms play an essential role in understanding the relationships between them. So let's take a look at some concrete examples.

Classification

The process of classification using KNN is relatively straightforward. We start by working with a dataset where each sample is assigned a label. To predict the label of a new sample, we compute the distance between it and all the other samples in the dataset. Next, we select only the $k$ closest samples based on the distance metric, where $k$ is a user-defined parameter. We then examine the labels of these $k$ samples and choose the label that appears most frequently. This label is assigned as the predicted label for the new sample.

Let's first grasp how kNN works visually with a small example.

data =
  DF.new(
    x: [-1, 0.2, -0.5, -2.1, -2.3, -2.2, 0.1, 0.3, 0.4, 0.7, 1.3],
    y: [-0.1, 0.4, 0.5, 0.4, 1.1, -1.0, -0.1, 0.2, 1.5, 1.6, 0.9],
    label: [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
  )

point_to_predict = DF.new(x: [0.0], y: [0.0])

k_eq_3 = DF.new(x: [0.45], y: [0.45], name: ["k = 3"])
k_eq_5 = DF.new(x: [0.72], y: [0.72], name: ["k = 5"])

radius = fn x, y -> :math.sqrt(x ** 2 + y ** 2) end

Tucan.layers([
  Tucan.scatter(data, "x", "y",
    point_size: 200,
    filled: true,
    shape_by: "label",
    color_by: "label"
  )
  |> Tucan.Scale.set_color_scheme(:plasma),
  Tucan.scatter(point_to_predict, "x", "y",
    point_size: 400,
    point_color: "green",
    point_shape: "triangle-up",
    filled: true
  ),
  Tucan.Geometry.circle({0, 0}, radius.(0.2, 0.4), line_color: "brown", stroke_width: 2),
  Tucan.Geometry.circle({0, 0}, radius.(-1, 0.1), line_color: "blue", stroke_width: 2),
  Tucan.annotate(Tucan.new(), 0.42, 0.42, "k = 3", color: "brown", size: 20),
  Tucan.annotate(Tucan.new(), 0.81, 0.81, "k = 5", color: "blue", size: 20)
])
|> Tucan.Scale.set_xy_domain(-2.4, 1.7)
|> Tucan.Grid.set_enabled(false)
|> Tucan.set_size(630, 630)
|> Tucan.set_title("Scatterplot showing KNN prediction process", offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","height":630,"layer":[{"data":{"values":[{"label":0,"x":-1.0,"y":-0.1},{"label":0,"x":0.2,"y":0.4},{"label":0,"x":-0.5,"y":0.5},{"label":0,"x":-2.1,"y":0.4},{"label":0,"x":-2.3,"y":1.1},{"label":0,"x":-2.2,"y":-1.0},{"label":1,"x":0.1,"y":-0.1},{"label":1,"x":0.3,"y":0.2},{"label":1,"x":0.4,"y":1.5},{"label":1,"x":0.7,"y":1.6},{"label":1,"x":1.3,"y":0.9}]},"encoding":{"color":{"field":"label","scale":{"reverse":false,"scheme":"plasma"},"type":"nominal"},"shape":{"field":"label","type":"nominal"},"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7],"zero":false},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7],"zero":false},"type":"quantitative"}},"mark":{"fillOpacity":1,"filled":true,"size":200,"type":"point"}},{"data":{"values":[{"x":0.0,"y":0.0}]},"encoding":{"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7],"zero":false},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7],"zero":false},"type":"quantitative"}},"mark":{"color":"green","fillOpacity":1,"filled":true,"shape":"triangle-up","size":400,"type":"point"}},{"data":{"sequence":{"as":"theta","start":0,"step":0.1,"stop":361}},"encoding":{"order":{"field":"theta"},"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7]},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7]},"type":"quantitative"}},"mark":{"color":"brown","fillOpacity":1,"strokeOpacity":1,"strokeWidth":2,"type":"line"},"transform":[{"as":"x","calculate":"0 + cos(datum.theta*PI/180) * 0.447213595499958"},{"as":"y","calculate":"0 + sin(datum.theta*PI/180) * 0.447213595499958"}]},{"data":{"sequence":{"as":"theta","start":0,"step":0.1,"stop":361}},"encoding":{"order":{"field":"theta"},"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7]},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7]},"type":"quantitative"}},"mark":{"color":"blue","fillOpacity":1,"strokeOpacity":1,"strokeWidth":2,"type":"line"},"transform":[{"as":"x","calculate":"0 + cos(datum.theta*PI/180) * 1.004987562112089"},{"as":"y","calculate":"0 + sin(datum.theta*PI/180) * 1.004987562112089"}]},{"data":{"values":[{"x":0.42,"y":0.42}]},"encoding":{"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7]},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7]},"type":"quantitative"}},"mark":{"color":"brown","size":20,"text":"k = 3","type":"text"}},{"data":{"values":[{"x":0.81,"y":0.81}]},"encoding":{"x":{"axis":{"grid":false},"field":"x","scale":{"domain":[-2.4,1.7]},"type":"quantitative"},"y":{"axis":{"grid":false},"field":"y","scale":{"domain":[-2.4,1.7]},"type":"quantitative"}},"mark":{"color":"blue","size":20,"text":"k = 5","type":"text"}}],"title":{"offset":20,"text":"Scatterplot showing KNN prediction process"},"width":630}

Note that the final prediction may vary depending on the value of $k$. For example, with $k = 3$, we would predict the green triangle as an orange square (1), whereas with $k = 5$, the purple circle (0) would be the final prediction.

Let's now test this using Scholar code. First, we will define our data.

x = Nx.stack(DF.discard(data, "label"), axis: 1)
labels = Nx.stack(DF.select(data, "label"), axis: 1) |> Nx.squeeze(axes: [1])
x_pred = Nx.stack(point_to_predict, axis: 1)

#Nx.Tensor<
  f64[1][2]
  EXLA.Backend<host:0, 0.3809581470.3464101900.76826>
  [
    [0.0, 0.0]
  ]
>

Let's now try with $k = 3$.

model = KNNClassifier.fit(x, labels, num_classes: 2, num_neighbors: 3, algorithm: :brute)
KNNClassifier.predict(model, x_pred)

#Nx.Tensor<
  s64[1]
  EXLA.Backend<host:0, 0.3809581470.3464101900.76922>
  [1]
>

And $k = 5$.

model = KNNClassifier.fit(x, labels, num_classes: 2, num_neighbors: 5, algorithm: :brute)
KNNClassifier.predict(model, x_pred)

#Nx.Tensor<
  s64[1]
  EXLA.Backend<host:0, 0.3809581470.3464101900.77007>
  [0]
>

As we can see, the predictions match our intuition from analyzing the plot.

Now, let's try KNN on a more complicated dataset: the Wine dataset. Our task will be to classify the quality of the wine. Before we load the dataset into Explorer.DataFrame for more efficient exploration, let's check some more detailed information about the dataset.

info =
  Req.get!(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality.names"
  ).body

Kino.Markdown.new(info)

data =
  Req.get!(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv"
  ).body

df_data = DF.load_csv!(data, delimiter: ";", dtypes: %{"total sulfur dioxide": :float})
tensor_data = Nx.stack(df_data, axis: 1)
df_data

#Explorer.DataFrame<
  Polars[4898 x 12]
  fixed acidity f64 [7.0, 6.3, 8.1, 7.2, 7.2, ...]
  volatile acidity f64 [0.27, 0.3, 0.28, 0.23, 0.23, ...]
  citric acid f64 [0.36, 0.34, 0.4, 0.32, 0.32, ...]
  residual sugar f64 [20.7, 1.6, 6.9, 8.5, 8.5, ...]
  chlorides f64 [0.045, 0.049, 0.05, 0.058, 0.058, ...]
  free sulfur dioxide f64 [45.0, 14.0, 30.0, 47.0, 47.0, ...]
  total sulfur dioxide f64 [170.0, 132.0, 97.0, 186.0, 186.0, ...]
  density f64 [1.001, 0.994, 0.9951, 0.9956, 0.9956, ...]
  pH f64 [3.0, 3.3, 3.26, 3.19, 3.19, ...]
  sulphates f64 [0.45, 0.49, 0.44, 0.4, 0.4, ...]
  alcohol f64 [8.8, 9.5, 10.1, 9.9, 9.9, ...]
  quality s64 [6, 6, 6, 6, 6, ...]
>

As we can see, there are no null values in the dataset. Now, let's check the size of the dataset.

DF.shape(df_data)

{4898, 12}

Let's check some statistical properties of the dataset. We will start with skewness, which measures the asymmetry of the probability distribution of a random variable about its mean. To better understand this concept, please take a look at the picture below.

Figure 1: A general relationship of mean and median under differently skewed unimodal distribution

Now, let's check the skewness of our dataset using Scholar.Stats.skew/1 function.

Scholar.Stats.skew(tensor_data)

#Nx.Tensor<
  f64[12]
  EXLA.Backend<host:0, 0.3809581470.3464101900.77136>
  [0.6475530855160632, 1.5764965159574844, 1.2815277799152376, 1.0767638711454446, 5.0217921696710315, 1.4063140718346212, 0.3905901775815236, 0.9774735389046988, 0.45764233925379794, 0.9768943947733456, 0.4871927332763434, 0.15574868141362447]
>

As we can see, all features have positive skewness, which means that their distributions are more similar to the left plot in the picture above.

Moving on to another statistical function, let's discuss kurtosis. Kurtosis measures how much data is located in the tails of distributions. If the kurtosis is greater than 0, the distribution is said to be "platykurtic", indicating that it has more extreme values than a univariate normal distribution. Similarly, a "leptokurtic" distribution has positive kurtosis and less extreme values, while a "mesokurtic" distribution has the same kurtosis as a normal distribution. Let's check the kurtosis of our dataset.

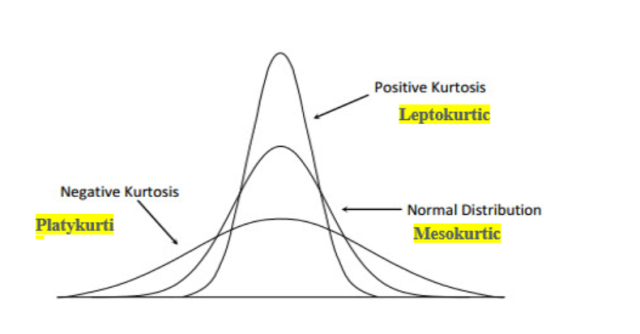Figure 2: Plot showing Platykurtic, Mesokurtic and Leptokurtic distributions

Scholar.Stats.kurtosis(tensor_data)

#Nx.Tensor<
  f64[12]
  EXLA.Backend<host:0, 0.3809581470.3464101900.77187>
  [2.168736944824719, 5.08520490451785, 6.167374226819426, 3.4650542966046363, 37.52503905008619, 11.453415905047144, 0.5700448984658735, 9.78258726703508, 0.5290085383907339, 1.5880812942840778, -0.6989373013774784, 0.21508011570192975]
>

Almost all features have positive kurtosis (they are leptokurtic). alcohol has negative excess kurtosis, which means it is platykurtic. Below there is Kernel Density Estimate (KDE) to check how exactly this tail look like.

# Increase the sample size (or use 1.0 to plot all data)
sample = DF.sample(df_data, 0.5, seed: seed)

Tucan.hconcat([
  Tucan.density(sample, "alcohol", only: ["alcohol"], fill_color: "lightblue")
  |> Tucan.Axes.set_x_title("% of alcohol")
  |> Tucan.set_size(350, 300)
  |> Tucan.set_title("KDE plot of alcohol feature", offset: 20),
  Tucan.density(sample, "pH", only: ["pH"], fill_color: "lightgreen")
  |> Tucan.set_size(350, 300)
  |> Tucan.set_title("KDE plot of pH feature", offset: 20)
])
|> Tucan.set_title("KDE plots of Features", anchor: :middle, offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","hconcat":[{"data":{"values":[{"alcohol":11.2},{"alcohol":11.2},{"alcohol":11.2},{"alcohol":10.2},{"alcohol":12.2},{"alcohol":9.5},{"alcohol":9.5},{"alcohol":10.7},{"alcohol":12.4},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":9.3},{"alcohol":8.9},{"alcohol":10.4},{"alcohol":12.8},{"alcohol":12.8},{"alcohol":8.9},{"alcohol":9.8},{"alcohol":8.9},{"alcohol":11.0666666666667},{"alcohol":10.8},{"alcohol":10.2},{"alcohol":9.0},{"alcohol":10.7},{"alcohol":9.4},{"alcohol":9.8},{"alcohol":8.0},{"alcohol":8.8},{"alcohol":9.9},{"alcohol":12.8},{"alcohol":10.4},{"alcohol":10.2},{"alcohol":10.6},{"alcohol":12.7},{"alcohol":12.9},{"alcohol":11.6},{"alcohol":12.0},{"alcohol":9.0},{"alcohol":10.0},{"alcohol":9.9},{"alcohol":9.1},{"alcohol":12.4},{"alcohol":11.1},{"alcohol":9.9},{"alcohol":9.6},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":9.4},{"alcohol":10.4},{"alcohol":9.6},{"alcohol":9.9},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":10.1},{"alcohol":8.8},{"alcohol":10.5},{"alcohol":12.9},{"alcohol":10.2},{"alcohol":11.6333333333333},{"alcohol":12.4},{"alcohol":9.0},{"alcohol":10.6},{"alcohol":9.9},{"alcohol":9.0},{"alcohol":11.4},{"alcohol":13.5},{"alcohol":9.53333333333333},{"alcohol":12.5},{"alcohol":10.6},{"alcohol":9.7},{"alcohol":10.4},{"alcohol":10.4},{"alcohol":12.2},{"alcohol":11.0},{"alcohol":11.9},{"alcohol":10.0},{"alcohol":10.4},{"alcohol":9.9},{"alcohol":10.7},{"alcohol":10.0},{"alcohol":9.8},{"alcohol":9.2},{"alcohol":8.7},{"alcohol":12.1},{"alcohol":11.2},{"alcohol":9.7},{"alcohol":10.4},{"alcohol":11.1},{"alcohol":11.5},{"alcohol":9.9},{"alcohol":9.6},{"alcohol":12.1},{"alcohol":11.5},{"alcohol":12.3},{"alcohol":9.2},{"alcohol":10.5},{"alcohol":11.9},{"alcohol":10.6},{"alcohol":12.4},{"alcohol":9.7},{"alcohol":9.0},{"alcohol":12.5},{"alcohol":9.2},{"alcohol":10.8},{"alcohol":9.1},{"alcohol":9.7},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":10.4},{"alcohol":12.7},{"alcohol":12.8},{"alcohol":8.8},{"alcohol":9.9},{"alcohol":11.3},{"alcohol":10.9},{"alcohol":9.3},{"alcohol":9.8},{"alcohol":13.5},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":8.8},{"alcohol":12.3},{"alcohol":11.5},{"alcohol":9.9},{"alcohol":11.9},{"alcohol":9.6},{"alcohol":12.1},{"alcohol":11.4},{"alcohol":12.8},{"alcohol":8.9},{"alcohol":10.3},{"alcohol":10.6},{"alcohol":10.7},{"alcohol":9.8},{"alcohol":11.7},{"alcohol":9.0},{"alcohol":10.3},{"alcohol":8.7},{"alcohol":9.2},{"alcohol":12.3},{"alcohol":9.6},{"alcohol":9.3},{"alcohol":9.4},{"alcohol":11.2},{"alcohol":10.2},{"alcohol":10.1},{"alcohol":9.3},{"alcohol":9.8},{"alcohol":9.0},{"alcohol":8.8},{"alcohol":10.9},{"alcohol":10.7},{"alcohol":12.0},{"alcohol":11.0},{"alcohol":12.9},{"alcohol":9.5},{"alcohol":10.2},{"alcohol":11.2666666666667},{"alcohol":9.4},{"alcohol":10.8},{"alcohol":9.6},{"alcohol":11.4},{"alcohol":8.7},{"alcohol":12.5},{"alcohol":12.0},{"alcohol":13.0},{"alcohol":9.4},{"alcohol":10.7},{"alcohol":10.0},{"alcohol":9.2},{"alcohol":9.8},{"alcohol":9.1},{"alcohol":9.9},{"alcohol":8.9},{"alcohol":10.2},{"alcohol":9.7},{"alcohol":9.5},{"alcohol":8.8},{"alcohol":11.6},{"alcohol":11.45},{"alcohol":11.5},{"alcohol":9.4},{"alcohol":8.7},{"alcohol":9.6},{"alcohol":11.4},{"alcohol":12.3},{"alcohol":11.0},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":9.8},{"alcohol":11.2},{"alcohol":12.8},{"alcohol":9.6},{"alcohol":10.0},{"alcohol":9.0},{"alcohol":12.0},{"alcohol":10.7},{"alcohol":11.3333333333333},{"alcohol":10.0},{"alcohol":11.5},{"alcohol":9.1},{"alcohol":9.0},{"alcohol":9.0},{"alcohol":11.0},{"alcohol":9.4},{"alcohol":11.2},{"alcohol":8.7},{"alcohol":9.6},{"alcohol":9.9},{"alcohol":12.5},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":10.5},{"alcohol":8.8},{"alcohol":9.3},{"alcohol":12.8},{"alcohol":9.1},{"alcohol":8.7},{"alcohol":8.6},{"alcohol":8.8},{"alcohol":10.3},{"alcohol":9.7},{"alcohol":9.5},{"alcohol":12.1},{"alcohol":12.0},{"alcohol":12.0},{"alcohol":10.5},{"alcohol":9.5},{"alcohol":8.6},{"alcohol":13.0},{"alcohol":9.3},{"alcohol":10.8},{"alcohol":9.75},{"alcohol":9.9},{"alcohol":9.1},{"alcohol":10.4},{"alcohol":11.5},{"alcohol":11.9},{"alcohol":9.4},{"alcohol":12.2},{"alcohol":8.6},{"alcohol":10.1},{"alcohol":11.2},{"alcohol":11.3},{"alcohol":13.4},{"alcohol":10.9},{"alcohol":10.1},{"alcohol":9.3},{"alcohol":11.5},{"alcohol":11.9},{"alcohol":8.9},{"alcohol":10.4},{"alcohol":9.6},{"alcohol":10.8},{"alcohol":12.5},{"alcohol":9.8},{"alcohol":9.1},{"alcohol":8.7},{"alcohol":11.2},{"alcohol":9.7},{"alcohol":10.7},{"alcohol":9.6},{"alcohol":12.5},{"alcohol":11.5},{"alcohol":9.7},{"alcohol":11.3},{"alcohol":12.1},{"alcohol":10.8},{"alcohol":10.8},{"alcohol":10.8},{"alcohol":11.4},{"alcohol":12.3},{"alcohol":10.8},{"alcohol":10.4},{"alcohol":8.7},{"alcohol":11.4},{"alcohol":12.8},{"alcohol":12.0},{"alcohol":10.5},{"alcohol":12.2},{"alcohol":9.7},{"alcohol":9.2},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":10.8},{"alcohol":9.6},{"alcohol":10.5},{"alcohol":12.6},{"alcohol":10.2},{"alcohol":10.3},{"alcohol":12.1},{"alcohol":12.2},{"alcohol":11.2},{"alcohol":10.7},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":12.2},{"alcohol":9.2},{"alcohol":10.2},{"alcohol":10.5},{"alcohol":10.4},{"alcohol":12.7},{"alcohol":10.0},{"alcohol":9.5},{"alcohol":10.0},{"alcohol":9.4},{"alcohol":10.2},{"alcohol":9.5},{"alcohol":11.0},{"alcohol":11.4},{"alcohol":10.5},{"alcohol":11.1},{"alcohol":8.4},{"alcohol":11.2},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":13.6},{"alcohol":9.4},{"alcohol":10.0},{"alcohol":12.0},{"alcohol":11.1},{"alcohol":12.5},{"alcohol":11.8},{"alcohol":10.0},{"alcohol":8.5},{"alcohol":10.2},{"alcohol":8.7},{"alcohol":11.4},{"alcohol":9.9},{"alcohol":12.8},{"alcohol":9.9},{"alcohol":9.4},{"alcohol":10.2},{"alcohol":8.8},{"alcohol":9.4},{"alcohol":9.7},{"alcohol":11.3},{"alcohol":9.2},{"alcohol":11.3},{"alcohol":11.2},{"alcohol":13.4},{"alcohol":13.5},{"alcohol":12.8},{"alcohol":10.2},{"alcohol":10.9},{"alcohol":11.5},{"alcohol":8.8},{"alcohol":11.0},{"alcohol":9.4},{"alcohol":10.3},{"alcohol":9.9},{"alcohol":8.9},{"alcohol":10.1},{"alcohol":10.1},{"alcohol":10.7},{"alcohol":11.1},{"alcohol":11.3},{"alcohol":11.1},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":10.4},{"alcohol":9.1},{"alcohol":8.8},{"alcohol":9.6},{"alcohol":10.5},{"alcohol":9.9},{"alcohol":11.3},{"alcohol":10.5},{"alcohol":9.1},{"alcohol":12.1},{"alcohol":10.4},{"alcohol":8.9},{"alcohol":11.0},{"alcohol":12.2},{"alcohol":9.5},{"alcohol":9.1},{"alcohol":9.5},{"alcohol":10.6},{"alcohol":10.6},{"alcohol":11.3},{"alcohol":8.7},{"alcohol":10.5},{"alcohol":8.8},{"alcohol":10.1},{"alcohol":11.2},{"alcohol":11.2},{"alcohol":9.2},{"alcohol":9.8},{"alcohol":10.0},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":11.9},{"alcohol":10.0},{"alcohol":11.2},{"alcohol":10.6},{"alcohol":12.1},{"alcohol":10.1},{"alcohol":11.0},{"alcohol":11.2},{"alcohol":9.5},{"alcohol":10.6},{"alcohol":9.5},{"alcohol":9.8},{"alcohol":13.7},{"alcohol":12.8},{"alcohol":12.0},{"alcohol":10.6},{"alcohol":9.5},{"alcohol":12.5},{"alcohol":10.5},{"alcohol":12.5},{"alcohol":9.5},{"alcohol":9.6},{"alcohol":9.3},{"alcohol":8.7},{"alcohol":12.2},{"alcohol":8.9},{"alcohol":11.0},{"alcohol":10.7},{"alcohol":8.9},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":9.1},{"alcohol":10.2},{"alcohol":11.8},{"alcohol":10.5},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":8.7},{"alcohol":10.5},{"alcohol":10.2},{"alcohol":12.5},{"alcohol":10.1},{"alcohol":11.3},{"alcohol":11.1},{"alcohol":12.2},{"alcohol":12.4},{"alcohol":10.9},{"alcohol":9.7},{"alcohol":9.0},{"alcohol":9.4},{"alcohol":10.3},{"alcohol":9.6},{"alcohol":9.0},{"alcohol":9.7},{"alcohol":9.8},{"alcohol":10.0},{"alcohol":11.0},{"alcohol":11.0},{"alcohol":10.8},{"alcohol":12.6},{"alcohol":9.5},{"alcohol":9.0},{"alcohol":10.0},{"alcohol":11.0},{"alcohol":10.9},{"alcohol":11.2},{"alcohol":13.2},{"alcohol":9.9},{"alcohol":11.4},{"alcohol":9.2},{"alcohol":11.4},{"alcohol":9.6},{"alcohol":9.2},{"alcohol":12.2},{"alcohol":9.6},{"alcohol":9.5},{"alcohol":12.1},{"alcohol":9.7},{"alcohol":9.7},{"alcohol":10.0},{"alcohol":10.5},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":12.0},{"alcohol":8.8},{"alcohol":8.8},{"alcohol":9.4},{"alcohol":9.9},{"alcohol":11.3},{"alcohol":9.9},{"alcohol":9.8},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":10.5},{"alcohol":12.3},{"alcohol":10.5},{"alcohol":10.7},{"alcohol":11.6},{"alcohol":11.8},{"alcohol":10.4},{"alcohol":11.4},{"alcohol":11.0},{"alcohol":9.7},{"alcohol":9.2},{"alcohol":11.1},{"alcohol":10.4},{"alcohol":12.9},{"alcohol":10.5},{"alcohol":9.9},{"alcohol":12.7},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":12.0},{"alcohol":11.0},{"alcohol":10.6},{"alcohol":11.3},{"alcohol":11.5},{"alcohol":9.5},{"alcohol":10.0},{"alcohol":9.2},{"alcohol":8.4},{"alcohol":9.4},{"alcohol":9.4},{"alcohol":9.4},{"alcohol":11.7},{"alcohol":13.3},{"alcohol":9.2},{"alcohol":10.1},{"alcohol":11.9},{"alcohol":11.2},{"alcohol":8.8},{"alcohol":9.1},{"alcohol":11.2},{"alcohol":12.0},{"alcohol":10.3},{"alcohol":10.4},{"alcohol":13.2},{"alcohol":11.7},{"alcohol":11.3},{"alcohol":10.2},{"alcohol":9.3},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":9.8},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":10.1},{"alcohol":8.9},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":12.8},{"alcohol":12.3},{"alcohol":12.6},{"alcohol":9.55},{"alcohol":9.0},{"alcohol":9.8},{"alcohol":11.1},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":9.8},{"alcohol":9.2},{"alcohol":10.0},{"alcohol":11.9},{"alcohol":9.2},{"alcohol":12.5},{"alcohol":13.1},{"alcohol":9.8},{"alcohol":11.0},{"alcohol":9.2},{"alcohol":8.9},{"alcohol":9.7},{"alcohol":11.6},{"alcohol":9.1},{"alcohol":12.6},{"alcohol":12.2},{"alcohol":8.6},{"alcohol":9.5},{"alcohol":11.2},{"alcohol":10.15},{"alcohol":9.3},{"alcohol":10.2},{"alcohol":11.8},{"alcohol":10.5},{"alcohol":9.2},{"alcohol":11.8},{"alcohol":9.8},{"alcohol":11.4},{"alcohol":11.8},{"alcohol":12.4},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":10.2},{"alcohol":12.2},{"alcohol":11.8},{"alcohol":9.5},{"alcohol":10.2},{"alcohol":10.9},{"alcohol":9.9},{"alcohol":11.1},{"alcohol":11.5},{"alcohol":11.5},{"alcohol":12.5},{"alcohol":9.3},{"alcohol":9.7},{"alcohol":11.4},{"alcohol":8.8},{"alcohol":12.0},{"alcohol":10.5},{"alcohol":12.0},{"alcohol":9.1},{"alcohol":10.0},{"alcohol":13.7},{"alcohol":9.6},{"alcohol":10.5},{"alcohol":9.5},{"alcohol":13.05},{"alcohol":9.6},{"alcohol":12.1},{"alcohol":12.3},{"alcohol":9.6},{"alcohol":12.4},{"alcohol":11.5},{"alcohol":8.9},{"alcohol":9.2},{"alcohol":12.6},{"alcohol":13.0},{"alcohol":10.9666666666667},{"alcohol":9.8},{"alcohol":10.0},{"alcohol":11.1},{"alcohol":10.4},{"alcohol":11.5},{"alcohol":11.9},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":10.0},{"alcohol":9.0},{"alcohol":9.9},{"alcohol":11.5},{"alcohol":12.9},{"alcohol":9.2},{"alcohol":9.8},{"alcohol":8.7},{"alcohol":11.4},{"alcohol":9.8},{"alcohol":11.8},{"alcohol":8.8},{"alcohol":9.3},{"alcohol":9.7},{"alcohol":11.3},{"alcohol":11.0},{"alcohol":10.1},{"alcohol":12.3},{"alcohol":9.2},{"alcohol":10.6},{"alcohol":11.8},{"alcohol":9.0},{"alcohol":9.2},{"alcohol":9.3},{"alcohol":10.1},{"alcohol":10.5},{"alcohol":10.5},{"alcohol":12.2},{"alcohol":9.1},{"alcohol":10.6},{"alcohol":13.4},{"alcohol":9.9},{"alcohol":10.5666666666667},{"alcohol":9.7},{"alcohol":10.3},{"alcohol":10.4},{"alcohol":10.9},{"alcohol":10.6},{"alcohol":11.3},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":12.7},{"alcohol":8.8},{"alcohol":9.5},{"alcohol":11.3},{"alcohol":10.9},{"alcohol":10.6},{"alcohol":8.9},{"alcohol":8.9},{"alcohol":12.7},{"alcohol":10.1},{"alcohol":11.7},{"alcohol":8.7},{"alcohol":8.9},{"alcohol":9.5},{"alcohol":9.2},{"alcohol":10.6},{"alcohol":9.0},{"alcohol":8.8},{"alcohol":10.7},{"alcohol":11.3},{"alcohol":11.9},{"alcohol":9.4},{"alcohol":12.6},{"alcohol":12.3},{"alcohol":10.8},{"alcohol":10.0},{"alcohol":9.9},{"alcohol":11.0},{"alcohol":9.9},{"alcohol":9.1},{"alcohol":9.5},{"alcohol":10.1},{"alcohol":11.8},{"alcohol":10.6},{"alcohol":9.5},{"alcohol":11.3},{"alcohol":10.2},{"alcohol":10.5},{"alcohol":9.3},{"alcohol":12.5},{"alcohol":11.2},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":9.3},{"alcohol":11.0},{"alcohol":10.1},{"alcohol":12.8},{"alcohol":14.0},{"alcohol":9.1},{"alcohol":10.4},{"alcohol":10.7},{"alcohol":11.6},{"alcohol":8.8},{"alcohol":11.3},{"alcohol":12.7},{"alcohol":10.8},{"alcohol":10.3},{"alcohol":8.9},{"alcohol":9.3},{"alcohol":8.7},{"alcohol":8.7},{"alcohol":10.4},{"alcohol":11.3},{"alcohol":12.0},{"alcohol":9.9},{"alcohol":10.1},{"alcohol":11.0},{"alcohol":10.3},{"alcohol":11.0},{"alcohol":8.8},{"alcohol":8.8},{"alcohol":10.1},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":9.3},{"alcohol":12.4},{"alcohol":14.0},{"alcohol":11.1},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":10.8},{"alcohol":11.8},{"alcohol":10.4},{"alcohol":9.7},{"alcohol":9.8},{"alcohol":12.4},{"alcohol":11.0},{"alcohol":12.7},{"alcohol":10.4},{"alcohol":10.2},{"alcohol":12.0},{"alcohol":9.5},{"alcohol":8.7},{"alcohol":9.3},{"alcohol":8.7},{"alcohol":10.5},{"alcohol":9.0},{"alcohol":9.2},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":9.2},{"alcohol":9.4},{"alcohol":12.9},{"alcohol":10.0},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":9.3},{"alcohol":9.2},{"alcohol":12.0},{"alcohol":13.2},{"alcohol":9.6},{"alcohol":9.6},{"alcohol":9.4},{"alcohol":12.3},{"alcohol":9.5},{"alcohol":10.5},{"alcohol":8.9},{"alcohol":10.8},{"alcohol":10.0},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":10.2},{"alcohol":10.0},{"alcohol":11.3},{"alcohol":12.0},{"alcohol":10.6},{"alcohol":10.1},{"alcohol":9.2},{"alcohol":10.7},{"alcohol":11.5},{"alcohol":11.5},{"alcohol":11.1},{"alcohol":10.1},{"alcohol":9.1},{"alcohol":12.0},{"alcohol":8.8},{"alcohol":11.0},{"alcohol":10.6},{"alcohol":9.7},{"alcohol":12.2},{"alcohol":10.8},{"alcohol":11.3},{"alcohol":11.2},{"alcohol":8.7},{"alcohol":9.2},{"alcohol":10.3},{"alcohol":11.9},{"alcohol":9.9},{"alcohol":9.3},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":12.75},{"alcohol":9.4},{"alcohol":9.7},{"alcohol":9.8},{"alcohol":8.9},{"alcohol":11.0},{"alcohol":11.0},{"alcohol":10.6},{"alcohol":9.5},{"alcohol":10.0},{"alcohol":9.6},{"alcohol":9.1},{"alcohol":12.6},{"alcohol":10.9},{"alcohol":11.4},{"alcohol":10.8},{"alcohol":9.5},{"alcohol":12.5},{"alcohol":11.5},{"alcohol":12.4},{"alcohol":10.0},{"alcohol":9.6},{"alcohol":10.2},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":9.2},{"alcohol":12.0},{"alcohol":9.3},{"alcohol":8.8},{"alcohol":12.3},{"alcohol":9.5},{"alcohol":9.2},{"alcohol":9.4},{"alcohol":10.7},{"alcohol":10.7},{"alcohol":11.2},{"alcohol":10.1},{"alcohol":10.4},{"alcohol":10.7},{"alcohol":9.7},{"alcohol":11.1},{"alcohol":10.8},{"alcohol":10.3},{"alcohol":10.2},{"alcohol":10.7},{"alcohol":10.1},{"alcohol":11.6},{"alcohol":10.0},{"alcohol":11.7},{"alcohol":10.6},{"alcohol":9.4},{"alcohol":9.2},{"alcohol":11.4},{"alcohol":12.0},{"alcohol":9.3},{"alcohol":10.0},{"alcohol":11.3},{"alcohol":10.3},{"alcohol":11.9},{"alcohol":9.5},{"alcohol":10.5},{"alcohol":12.0},{"alcohol":11.2},{"alcohol":11.4},{"alcohol":12.3},{"alcohol":9.0},{"alcohol":11.4},{"alcohol":9.3},{"alcohol":8.6},{"alcohol":11.8},{"alcohol":11.2},{"alcohol":10.5},{"alcohol":13.6},{"alcohol":10.5},{"alcohol":9.8},{"alcohol":9.0},{"alcohol":9.1},{"alcohol":9.2},{"alcohol":9.3},{"alcohol":12.4},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":10.1},{"alcohol":11.7},{"alcohol":12.7},{"alcohol":10.4},{"alcohol":10.6},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":12.2},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":13.0},{"alcohol":11.2},{"alcohol":10.5},{"alcohol":10.5},{"alcohol":11.5},{"alcohol":13.1},{"alcohol":10.0},{"alcohol":9.6},{"alcohol":12.0},{"alcohol":12.9},{"alcohol":10.3},{"alcohol":10.5},{"alcohol":10.7},{"alcohol":10.4},{"alcohol":10.0},{"alcohol":12.9},{"alcohol":9.1},{"alcohol":12.5},{"alcohol":10.4},{"alcohol":12.3},{"alcohol":8.6},{"alcohol":9.8},{"alcohol":12.0},{"alcohol":10.6},{"alcohol":8.8},{"alcohol":11.0},{"alcohol":10.3},{"alcohol":11.4},{"alcohol":10.8},{"alcohol":12.9},{"alcohol":11.2},{"alcohol":13.0},{"alcohol":11.2},{"alcohol":11.5},{"alcohol":9.2},{"alcohol":11.4},{"alcohol":10.6},{"alcohol":11.6},{"alcohol":10.8},{"alcohol":9.3},{"alcohol":10.0},{"alcohol":11.3},{"alcohol":8.8},{"alcohol":10.2},{"alcohol":10.0},{"alcohol":9.5},{"alcohol":9.0},{"alcohol":10.8},{"alcohol":10.0},{"alcohol":10.6},{"alcohol":9.7},{"alcohol":11.4},{"alcohol":10.0},{"alcohol":11.4},{"alcohol":8.6},{"alcohol":12.5},{"alcohol":9.8},{"alcohol":10.2},{"alcohol":12.2},{"alcohol":9.55},{"alcohol":11.5},{"alcohol":13.2},{"alcohol":10.1},{"alcohol":11.9},{"alcohol":9.5},{"alcohol":10.7},{"alcohol":8.9},{"alcohol":11.5},{"alcohol":11.0},{"alcohol":12.2},{"alcohol":12.4},{"alcohol":10.8},{"alcohol":13.1},{"alcohol":9.3},{"alcohol":12.7},{"alcohol":11.4},{"alcohol":13.0},{"alcohol":10.2},{"alcohol":11.3},{"alcohol":9.4},{"alcohol":11.5},{"alcohol":11.6},{"alcohol":12.5},{"alcohol":10.0},{"alcohol":9.4},{"alcohol":8.7},{"alcohol":12.8},{"alcohol":11.3},{"alcohol":12.2},{"alcohol":10.0},{"alcohol":10.6},{"alcohol":9.1},{"alcohol":10.4},{"alcohol":11.0},{"alcohol":12.6},{"alcohol":9.4},{"alcohol":11.94},{"alcohol":10.4},{"alcohol":10.4},{"alcohol":9.1},{"alcohol":11.1},{"alcohol":9.9},{"alcohol":8.9},{"alcohol":8.8},{"alcohol":13.4},{"alcohol":13.1333333333333},{"alcohol":12.6},{"alcohol":10.5},{"alcohol":11.0},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":10.4},{"alcohol":11.2},{"alcohol":9.0},{"alcohol":11.3},{"alcohol":11.4},{"alcohol":9.4},{"alcohol":10.4},{"alcohol":11.5},{"alcohol":10.9},{"alcohol":12.2},{"alcohol":12.0},{"alcohol":9.4},{"alcohol":8.9},{"alcohol":8.8},{"alcohol":9.5},{"alcohol":9.6},{"alcohol":12.2},{"alcohol":11.2},{"alcohol":12.3},{"alcohol":9.9},{"alcohol":9.8},{"alcohol":11.1},{"alcohol":10.1},{"alcohol":9.2},{"alcohol":9.6},{"alcohol":9.4},{"alcohol":12.2},{"alcohol":9.2},{"alcohol":12.6},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":12.8},{"alcohol":10.4},{"alcohol":8.9},{"alcohol":10.0},{"alcohol":10.8},{"alcohol":10.2},{"alcohol":10.8},{"alcohol":11.1},{"alcohol":9.1},{"alcohol":9.2},{"alcohol":12.7},{"alcohol":9.7},{"alcohol":11.9},{"alcohol":9.6},{"alcohol":12.0},{"alcohol":12.5},{"alcohol":9.2},{"alcohol":9.7},{"alcohol":9.2},{"alcohol":11.2},{"alcohol":10.8},{"alcohol":13.4},{"alcohol":10.6},{"alcohol":11.4},{"alcohol":9.2},{"alcohol":12.2},{"alcohol":10.8},{"alcohol":10.7},{"alcohol":9.8},{"alcohol":11.4},{"alcohol":12.4},{"alcohol":10.8},{"alcohol":11.1},{"alcohol":10.9},{"alcohol":9.7},{"alcohol":10.8},{"alcohol":11.4},{"alcohol":10.5},{"alcohol":10.0},{"alcohol":10.3},{"alcohol":8.9},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":10.15},{"alcohol":11.9},{"alcohol":11.6},{"alcohol":8.9},{"alcohol":9.4},{"alcohol":11.3},{"alcohol":9.0},{"alcohol":8.9},{"alcohol":10.5},{"alcohol":9.8},{"alcohol":9.8},{"alcohol":9.5},{"alcohol":11.9},{"alcohol":10.0},{"alcohol":12.6},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":9.1},{"alcohol":10.1},{"alcohol":11.1},{"alcohol":10.9},{"alcohol":12.2},{"alcohol":10.7},{"alcohol":9.5},{"alcohol":12.7},{"alcohol":12.8},{"alcohol":9.3},{"alcohol":11.1},{"alcohol":12.6},{"alcohol":9.3},{"alcohol":9.3},{"alcohol":8.8},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":11.1},{"alcohol":10.8},{"alcohol":9.8},{"alcohol":10.9},{"alcohol":11.3},{"alcohol":9.3},{"alcohol":9.1},{"alcohol":9.6},{"alcohol":13.3},{"alcohol":12.4},{"alcohol":10.9},{"alcohol":10.5},{"alcohol":8.7},{"alcohol":9.0},{"alcohol":12.6},{"alcohol":13.0},{"alcohol":13.5},{"alcohol":10.0},{"alcohol":9.3},{"alcohol":12.5},{"alcohol":9.4},{"alcohol":13.0},{"alcohol":9.3},{"alcohol":9.1},{"alcohol":11.6},{"alcohol":10.9333333333333},{"alcohol":9.2},{"alcohol":11.0},{"alcohol":9.0},{"alcohol":9.6},{"alcohol":13.0},{"alcohol":12.1},{"alcohol":8.6},{"alcohol":10.4},{"alcohol":11.4},{"alcohol":10.5},{"alcohol":9.7},{"alcohol":8.8},{"alcohol":11.3},{"alcohol":10.3},{"alcohol":9.5},{"alcohol":11.4},{"alcohol":12.6},{"alcohol":10.6},{"alcohol":9.0},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":12.6},{"alcohol":10.9},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":11.7},{"alcohol":11.6},{"alcohol":9.4},{"alcohol":10.4},{"alcohol":10.8},{"alcohol":9.1},{"alcohol":12.4},{"alcohol":11.8},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":10.2},{"alcohol":10.8},{"alcohol":12.4},{"alcohol":11.2},{"alcohol":11.1},{"alcohol":10.8},{"alcohol":9.3},{"alcohol":10.0},{"alcohol":11.0},{"alcohol":8.9},{"alcohol":13.1},{"alcohol":10.9},{"alcohol":10.7},{"alcohol":10.3},{"alcohol":10.5},{"alcohol":10.6},{"alcohol":12.0},{"alcohol":8.8},{"alcohol":9.8},{"alcohol":11.1},{"alcohol":10.7},{"alcohol":8.9},{"alcohol":12.0},{"alcohol":10.4},{"alcohol":8.7},{"alcohol":11.5},{"alcohol":9.0},{"alcohol":8.8},{"alcohol":12.6},{"alcohol":11.6},{"alcohol":8.8},{"alcohol":12.2},{"alcohol":12.2},{"alcohol":10.8},{"alcohol":10.3},{"alcohol":10.2},{"alcohol":11.4},{"alcohol":10.5},{"alcohol":8.9},{"alcohol":10.4},{"alcohol":10.4},{"alcohol":9.5},{"alcohol":10.6},{"alcohol":11.0},{"alcohol":10.1},{"alcohol":12.4},{"alcohol":11.1},{"alcohol":11.4666666666667},{"alcohol":9.2},{"alcohol":10.0},{"alcohol":9.4},{"alcohol":8.7},{"alcohol":9.4},{"alcohol":12.5},{"alcohol":10.5},{"alcohol":11.7},{"alcohol":9.1},{"alcohol":10.1},{"alcohol":12.5},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":10.4},{"alcohol":12.5},{"alcohol":11.2},{"alcohol":9.5},{"alcohol":10.5},{"alcohol":11.2},{"alcohol":10.4},{"alcohol":9.53333333333333},{"alcohol":11.6},{"alcohol":12.6},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":11.1},{"alcohol":12.8},{"alcohol":9.9},{"alcohol":10.6},{"alcohol":9.1},{"alcohol":10.8},{"alcohol":11.7},{"alcohol":9.2},{"alcohol":13.4},{"alcohol":11.2},{"alcohol":11.8},{"alcohol":12.3},{"alcohol":11.0},{"alcohol":10.1},{"alcohol":9.9},{"alcohol":11.9},{"alcohol":9.9},{"alcohol":9.9},{"alcohol":10.4},{"alcohol":10.0},{"alcohol":12.2},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":9.1},{"alcohol":12.6},{"alcohol":12.2},{"alcohol":9.3},{"alcohol":12.8},{"alcohol":10.5},{"alcohol":9.2},{"alcohol":8.8},{"alcohol":10.9},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":12.6},{"alcohol":11.0},{"alcohol":9.0},{"alcohol":9.6},{"alcohol":11.1},{"alcohol":10.1},{"alcohol":12.5},{"alcohol":9.8},{"alcohol":10.6},{"alcohol":9.2},{"alcohol":11.6},{"alcohol":10.0},{"alcohol":11.4},{"alcohol":9.0},{"alcohol":10.5},{"alcohol":12.7},{"alcohol":10.4},{"alcohol":9.6},{"alcohol":9.4},{"alcohol":11.4},{"alcohol":8.8},{"alcohol":8.7},{"alcohol":10.2},{"alcohol":10.2},{"alcohol":9.1},{"alcohol":12.0},{"alcohol":10.8},{"alcohol":9.8},{"alcohol":12.8},{"alcohol":12.6},{"alcohol":10.6},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":8.5},{"alcohol":12.1},{"alcohol":11.0},{"alcohol":9.6},{"alcohol":10.4},{"alcohol":12.1},{"alcohol":10.8},{"alcohol":11.3},{"alcohol":11.5},{"alcohol":10.5},{"alcohol":12.1},{"alcohol":9.2},{"alcohol":9.6},{"alcohol":9.5},{"alcohol":11.4},{"alcohol":10.2},{"alcohol":9.0},{"alcohol":12.8},{"alcohol":11.1},{"alcohol":12.8},{"alcohol":10.7},{"alcohol":12.5},{"alcohol":9.6},{"alcohol":9.1},{"alcohol":12.2},{"alcohol":9.9},{"alcohol":9.4},{"alcohol":9.6},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":13.0},{"alcohol":11.5},{"alcohol":11.0},{"alcohol":10.1},{"alcohol":12.0},{"alcohol":9.8},{"alcohol":10.9},{"alcohol":10.4},{"alcohol":10.3},{"alcohol":8.8},{"alcohol":10.1},{"alcohol":9.5},{"alcohol":9.2},{"alcohol":12.3},{"alcohol":11.2},{"alcohol":9.5},{"alcohol":12.6},{"alcohol":10.0},{"alcohol":12.8933333333333},{"alcohol":11.5},{"alcohol":11.8},{"alcohol":9.2},{"alcohol":9.3},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":11.8},{"alcohol":11.2},{"alcohol":9.2},{"alcohol":11.3},{"alcohol":10.5},{"alcohol":11.3},{"alcohol":8.7},{"alcohol":10.0},{"alcohol":10.4},{"alcohol":10.9},{"alcohol":8.9},{"alcohol":12.0666666666667},{"alcohol":9.2},{"alcohol":11.0},{"alcohol":9.4},{"alcohol":11.5},{"alcohol":10.5},{"alcohol":10.2},{"alcohol":10.9},{"alcohol":8.8},{"alcohol":10.0},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":8.9},{"alcohol":9.6},{"alcohol":9.7},{"alcohol":10.3},{"alcohol":9.3},{"alcohol":10.3},{"alcohol":9.3},{"alcohol":11.6},{"alcohol":11.4},{"alcohol":12.3},{"alcohol":10.3},{"alcohol":9.3},{"alcohol":11.8},{"alcohol":8.9},{"alcohol":9.8},{"alcohol":9.8},{"alcohol":11.7},{"alcohol":9.0},{"alcohol":10.4},{"alcohol":12.5},{"alcohol":9.63333333333333},{"alcohol":11.5},{"alcohol":9.2},{"alcohol":8.8},{"alcohol":10.4},{"alcohol":12.5},{"alcohol":9.2},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":9.8},{"alcohol":9.6},{"alcohol":9.1},{"alcohol":9.8},{"alcohol":12.5},{"alcohol":9.9},{"alcohol":9.73333333333333},{"alcohol":14.0},{"alcohol":11.6},{"alcohol":11.0},{"alcohol":9.2},{"alcohol":11.3},{"alcohol":10.4},{"alcohol":10.5},{"alcohol":10.0},{"alcohol":9.4},{"alcohol":13.0},{"alcohol":10.8},{"alcohol":9.4},{"alcohol":11.6},{"alcohol":12.5},{"alcohol":10.7},{"alcohol":10.6},{"alcohol":10.7},{"alcohol":11.4},{"alcohol":9.2},{"alcohol":8.9},{"alcohol":10.55},{"alcohol":12.4},{"alcohol":10.8},{"alcohol":12.5},{"alcohol":9.4},{"alcohol":9.7},{"alcohol":9.4},{"alcohol":10.8},{"alcohol":10.4},{"alcohol":10.2},{"alcohol":12.1},{"alcohol":10.5},{"alcohol":9.2},{"alcohol":9.1},{"alcohol":11.4},{"alcohol":10.2},{"alcohol":11.2},{"alcohol":11.0},{"alcohol":11.4},{"alcohol":9.0},{"alcohol":9.3},{"alcohol":9.5},{"alcohol":10.0},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":12.2},{"alcohol":11.75},{"alcohol":9.4},{"alcohol":10.4},{"alcohol":10.6},{"alcohol":10.8},{"alcohol":10.9},{"alcohol":9.4},{"alcohol":11.2},{"alcohol":12.6},{"alcohol":10.2},{"alcohol":12.5},{"alcohol":8.8},{"alcohol":9.9},{"alcohol":10.9},{"alcohol":11.3},{"alcohol":10.8},{"alcohol":9.9},{"alcohol":12.6},{"alcohol":10.5},{"alcohol":10.5},{"alcohol":11.0},{"alcohol":9.0},{"alcohol":9.4},{"alcohol":12.0},{"alcohol":10.4},{"alcohol":11.4},{"alcohol":11.4},{"alcohol":10.7},{"alcohol":10.5},{"alcohol":12.6},{"alcohol":12.8933333333333},{"alcohol":11.8},{"alcohol":9.6},{"alcohol":9.8},{"alcohol":9.4},{"alcohol":13.1},{"alcohol":12.0},{"alcohol":10.1},{"alcohol":11.7},{"alcohol":10.7},{"alcohol":11.1},{"alcohol":12.2},{"alcohol":10.4},{"alcohol":11.9},{"alcohol":10.3},{"alcohol":10.4},{"alcohol":10.8},{"alcohol":10.0},{"alcohol":9.5},{"alcohol":10.3},{"alcohol":10.5},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":12.0},{"alcohol":10.4},{"alcohol":9.0},{"alcohol":8.6},{"alcohol":13.6},{"alcohol":9.4},{"alcohol":9.1},{"alcohol":9.1},{"alcohol":11.5},{"alcohol":10.0},{"alcohol":13.1},{"alcohol":10.5},{"alcohol":10.5},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":10.0},{"alcohol":12.7},{"alcohol":11.2},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":10.5},{"alcohol":12.7},{"alcohol":11.4},{"alcohol":12.7},{"alcohol":11.2},{"alcohol":10.6},{"alcohol":9.4},{"alcohol":10.1},{"alcohol":10.1},{"alcohol":9.5},{"alcohol":11.0},{"alcohol":9.0},{"alcohol":11.6},{"alcohol":9.0},{"alcohol":10.2},{"alcohol":10.3},{"alcohol":11.7},{"alcohol":11.2},{"alcohol":10.2},{"alcohol":12.6},{"alcohol":11.7},{"alcohol":9.4},{"alcohol":9.8},{"alcohol":11.4},{"alcohol":10.7},{"alcohol":9.9},{"alcohol":10.1},{"alcohol":11.9},{"alcohol":10.5},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":14.05},{"alcohol":12.2},{"alcohol":12.1},{"alcohol":9.0},{"alcohol":10.7},{"alcohol":12.7},{"alcohol":12.5},{"alcohol":10.0},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":9.7},{"alcohol":9.5},{"alcohol":13.7},{"alcohol":9.7},{"alcohol":12.4},{"alcohol":9.3},{"alcohol":12.0},{"alcohol":9.9},{"alcohol":11.5},{"alcohol":11.0},{"alcohol":11.4},{"alcohol":10.5},{"alcohol":11.3},{"alcohol":11.2},{"alcohol":10.4},{"alcohol":10.5},{"alcohol":13.3},{"alcohol":9.4},{"alcohol":9.7},{"alcohol":9.0},{"alcohol":8.8},{"alcohol":10.5},{"alcohol":9.6},{"alcohol":10.9},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":10.0},{"alcohol":12.0},{"alcohol":9.5},{"alcohol":9.7},{"alcohol":9.1},{"alcohol":10.6},{"alcohol":9.1},{"alcohol":9.2},{"alcohol":12.0},{"alcohol":9.6},{"alcohol":9.4},{"alcohol":12.4},{"alcohol":9.8},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":10.1333333333333},{"alcohol":9.1},{"alcohol":10.5},{"alcohol":10.7},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":9.3},{"alcohol":10.7},{"alcohol":11.5},{"alcohol":10.9},{"alcohol":10.7},{"alcohol":11.8},{"alcohol":8.8},{"alcohol":9.2},{"alcohol":9.0},{"alcohol":9.9},{"alcohol":9.5},{"alcohol":11.0},{"alcohol":13.3},{"alcohol":10.7},{"alcohol":10.0},{"alcohol":9.6},{"alcohol":10.2},{"alcohol":10.3},{"alcohol":9.8},{"alcohol":11.9},{"alcohol":9.4},{"alcohol":11.3},{"alcohol":10.1},{"alcohol":9.2},{"alcohol":11.5},{"alcohol":10.1},{"alcohol":10.0},{"alcohol":12.2},{"alcohol":10.1},{"alcohol":10.0},{"alcohol":11.0},{"alcohol":11.8},{"alcohol":11.1},{"alcohol":10.5},{"alcohol":8.9},{"alcohol":10.9},{"alcohol":9.3},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":8.9},{"alcohol":10.6},{"alcohol":11.7},{"alcohol":10.0},{"alcohol":13.8},{"alcohol":11.2},{"alcohol":10.5},{"alcohol":9.0},{"alcohol":10.2},{"alcohol":11.2},{"alcohol":9.3},{"alcohol":10.6},{"alcohol":12.1},{"alcohol":8.7},{"alcohol":11.6},{"alcohol":11.3},{"alcohol":11.5},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":9.6},{"alcohol":10.0},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":11.0},{"alcohol":10.0},{"alcohol":9.9},{"alcohol":12.0},{"alcohol":13.3},{"alcohol":11.3},{"alcohol":11.0},{"alcohol":11.0},{"alcohol":9.6},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":12.3},{"alcohol":11.5},{"alcohol":10.6},{"alcohol":10.8},{"alcohol":9.8},{"alcohol":9.8},{"alcohol":11.5},{"alcohol":11.2},{"alcohol":12.3},{"alcohol":11.2},{"alcohol":10.6},{"alcohol":12.5},{"alcohol":11.5},{"alcohol":11.1},{"alcohol":8.8},{"alcohol":10.0},{"alcohol":11.6},{"alcohol":11.2},{"alcohol":9.2},{"alcohol":10.7},{"alcohol":9.8},{"alcohol":11.0},{"alcohol":12.8},{"alcohol":12.7},{"alcohol":11.0},{"alcohol":13.4},{"alcohol":9.9},{"alcohol":9.2},{"alcohol":11.8},{"alcohol":9.7},{"alcohol":10.6},{"alcohol":11.1},{"alcohol":9.4},{"alcohol":12.2},{"alcohol":9.8},{"alcohol":9.5},{"alcohol":12.6},{"alcohol":9.9},{"alcohol":9.4},{"alcohol":11.4},{"alcohol":9.1},{"alcohol":9.3},{"alcohol":9.4},{"alcohol":9.9},{"alcohol":12.4},{"alcohol":9.6},{"alcohol":12.5},{"alcohol":12.1},{"alcohol":9.8},{"alcohol":9.3},{"alcohol":10.3},{"alcohol":9.3},{"alcohol":10.4},{"alcohol":11.9},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":11.5},{"alcohol":8.8},{"alcohol":10.8},{"alcohol":9.0},{"alcohol":9.2},{"alcohol":8.6},{"alcohol":8.7},{"alcohol":12.5},{"alcohol":10.1},{"alcohol":10.1},{"alcohol":11.9},{"alcohol":10.6},{"alcohol":11.2},{"alcohol":10.7},{"alcohol":9.8},{"alcohol":12.1},{"alcohol":9.2},{"alcohol":10.4},{"alcohol":11.2},{"alcohol":11.3},{"alcohol":10.2},{"alcohol":10.15},{"alcohol":12.6},{"alcohol":11.3},{"alcohol":11.8},{"alcohol":13.55},{"alcohol":12.5},{"alcohol":10.6},{"alcohol":10.9},{"alcohol":9.5},{"alcohol":9.2},{"alcohol":12.9},{"alcohol":12.3},{"alcohol":9.2},{"alcohol":10.6},{"alcohol":9.3},{"alcohol":12.9},{"alcohol":10.0},{"alcohol":12.9},{"alcohol":10.7},{"alcohol":9.5},{"alcohol":11.1},{"alcohol":10.4},{"alcohol":9.1},{"alcohol":9.4},{"alcohol":9.7},{"alcohol":11.3},{"alcohol":9.4},{"alcohol":11.0},{"alcohol":10.2},{"alcohol":9.4},{"alcohol":10.1},{"alcohol":9.0},{"alcohol":10.5},{"alcohol":11.1},{"alcohol":9.4},{"alcohol":9.4},{"alcohol":12.7},{"alcohol":9.2},{"alcohol":11.1},{"alcohol":11.2},{"alcohol":11.0},{"alcohol":11.8},{"alcohol":12.2},{"alcohol":12.4},{"alcohol":10.1},{"alcohol":9.5},{"alcohol":10.1},{"alcohol":9.1},{"alcohol":11.6},{"alcohol":10.0},{"alcohol":9.2},{"alcohol":9.0},{"alcohol":9.6},{"alcohol":11.8},{"alcohol":11.4},{"alcohol":11.7},{"alcohol":11.4},{"alcohol":11.9},{"alcohol":11.4},{"alcohol":9.3},{"alcohol":12.8},{"alcohol":11.3},{"alcohol":13.4},{"alcohol":9.0},{"alcohol":8.8},{"alcohol":12.6},{"alcohol":10.8},{"alcohol":12.9},{"alcohol":10.0},{"alcohol":10.4},{"alcohol":11.3},{"alcohol":10.6},{"alcohol":13.0},{"alcohol":9.2},{"alcohol":10.1333333333333},{"alcohol":9.4},{"alcohol":9.8},{"alcohol":11.8},{"alcohol":9.8},{"alcohol":9.1},{"alcohol":11.3},{"alcohol":12.4},{"alcohol":8.9},{"alcohol":8.9},{"alcohol":10.3},{"alcohol":11.0},{"alcohol":10.2},{"alcohol":9.5},{"alcohol":11.2},{"alcohol":9.6},{"alcohol":9.7},{"alcohol":9.0},{"alcohol":11.0},{"alcohol":12.6},{"alcohol":12.2},{"alcohol":12.3},{"alcohol":10.2},{"alcohol":9.6},{"alcohol":10.2},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":12.9},{"alcohol":9.8},{"alcohol":11.0},{"alcohol":9.5},{"alcohol":9.1},{"alcohol":10.0},{"alcohol":9.5},{"alcohol":12.5},{"alcohol":10.6},{"alcohol":11.1},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":11.4},{"alcohol":10.1},{"alcohol":12.7},{"alcohol":10.4},{"alcohol":10.5},{"alcohol":10.5},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":9.0},{"alcohol":11.05},{"alcohol":10.1},{"alcohol":9.0},{"alcohol":11.1},{"alcohol":10.5},{"alcohol":10.1},{"alcohol":9.2},{"alcohol":9.2},{"alcohol":9.2},{"alcohol":9.9},{"alcohol":9.4},{"alcohol":9.3},{"alcohol":10.3},{"alcohol":8.8},{"alcohol":9.4},{"alcohol":10.0},{"alcohol":9.3},{"alcohol":13.9},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":10.0},{"alcohol":10.5},{"alcohol":9.9},{"alcohol":13.4},{"alcohol":9.6},{"alcohol":10.0},{"alcohol":11.5},{"alcohol":11.4},{"alcohol":10.1},{"alcohol":11.3},{"alcohol":9.1},{"alcohol":12.6},{"alcohol":9.6},{"alcohol":11.8},{"alcohol":9.1},{"alcohol":9.0},{"alcohol":12.8},{"alcohol":9.5},{"alcohol":10.55},{"alcohol":10.4},{"alcohol":9.3},{"alcohol":8.7},{"alcohol":12.1},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":9.6},{"alcohol":11.9},{"alcohol":11.85},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":9.2},{"alcohol":11.3},{"alcohol":10.7},{"alcohol":10.3},{"alcohol":9.3},{"alcohol":10.5},{"alcohol":11.5},{"alcohol":10.5},{"alcohol":8.8},{"alcohol":10.8},{"alcohol":10.5},{"alcohol":10.0},{"alcohol":11.0},{"alcohol":9.3},{"alcohol":10.9},{"alcohol":11.4},{"alcohol":12.9},{"alcohol":8.7},{"alcohol":8.6},{"alcohol":9.1},{"alcohol":9.5},{"alcohol":10.7},{"alcohol":9.4},{"alcohol":9.2},{"alcohol":9.0},{"alcohol":9.2},{"alcohol":10.6},{"alcohol":11.1},{"alcohol":12.1},{"alcohol":12.2},{"alcohol":11.0},{"alcohol":9.5},{"alcohol":10.5},{"alcohol":9.8},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":11.2},{"alcohol":8.8},{"alcohol":10.3},{"alcohol":11.4},{"alcohol":9.1},{"alcohol":10.3},{"alcohol":13.6},{"alcohol":13.7},{"alcohol":11.3},{"alcohol":9.5},{"alcohol":9.9},{"alcohol":12.7},{"alcohol":9.5},{"alcohol":9.5},{"alcohol":12.0},{"alcohol":9.0},{"alcohol":9.8},{"alcohol":12.7},{"alcohol":10.1},{"alcohol":9.1},{"alcohol":8.6},{"alcohol":10.9},{"alcohol":12.1},{"alcohol":9.4},{"alcohol":9.6},{"alcohol":10.0},{"alcohol":10.7},{"alcohol":9.2},{"alcohol":9.1},{"alcohol":8.9},{"alcohol":10.4666666666667},{"alcohol":11.3},{"alcohol":11.2},{"alcohol":9.4},{"alcohol":13.5},{"alcohol":11.3},{"alcohol":11.0},{"alcohol":9.7},{"alcohol":12.8},{"alcohol":9.2},{"alcohol":10.8},{"alcohol":12.2},{"alcohol":12.4},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":10.8},{"alcohol":10.6},{"alcohol":11.9},{"alcohol":11.8},{"alcohol":11.0},{"alcohol":10.9},{"alcohol":9.4},{"alcohol":9.2},{"alcohol":8.9},{"alcohol":10.6},{"alcohol":13.7},{"alcohol":10.6},{"alcohol":11.3},{"alcohol":11.6},{"alcohol":9.8},{"alcohol":12.4},{"alcohol":10.4},{"alcohol":12.6},{"alcohol":12.1},{"alcohol":12.0},{"alcohol":12.8},{"alcohol":11.2},{"alcohol":10.8},{"alcohol":12.2},{"alcohol":10.3},{"alcohol":12.8},{"alcohol":9.6},{"alcohol":10.0},{"alcohol":12.1},{"alcohol":12.2},{"alcohol":9.3},{"alcohol":12.05},{"alcohol":8.8},{"alcohol":12.5},{"alcohol":10.2},{"alcohol":8.8},{"alcohol":9.0},{"alcohol":9.5},{"alcohol":11.1},{"alcohol":9.6},{"alcohol":13.0},{"alcohol":10.8},{"alcohol":12.5},{"alcohol":10.3},{"alcohol":9.8},{"alcohol":11.0},{"alcohol":8.7},{"alcohol":12.7},{"alcohol":11.3},{"alcohol":11.3},{"alcohol":10.3},{"alcohol":10.1},{"alcohol":9.2},{"alcohol":9.7},{"alcohol":12.1},{"alcohol":10.0},{"alcohol":13.1},{"alcohol":10.7},{"alcohol":10.3},{"alcohol":9.2},{"alcohol":9.4},{"alcohol":9.9},{"alcohol":14.2},{"alcohol":9.8},{"alcohol":11.8},{"alcohol":11.0},{"alcohol":10.5},{"alcohol":9.5},{"alcohol":9.4},{"alcohol":13.2},{"alcohol":12.3},{"alcohol":10.8},{"alcohol":9.4},{"alcohol":11.9},{"alcohol":10.0},{"alcohol":9.1},{"alcohol":10.3},{"alcohol":11.9},{"alcohol":10.8},{"alcohol":10.9},{"alcohol":9.0},{"alcohol":10.6},{"alcohol":8.8},{"alcohol":9.2},{"alcohol":9.6},{"alcohol":9.0},{"alcohol":12.2},{"alcohol":10.8},{"alcohol":11.4},{"alcohol":12.9},{"alcohol":11.8},{"alcohol":9.2},{"alcohol":9.3},{"alcohol":9.8},{"alcohol":10.3},{"alcohol":9.9},{"alcohol":9.3},{"alcohol":12.1},{"alcohol":9.5},{"alcohol":9.9},{"alcohol":11.1},{"alcohol":11.5},{"alcohol":11.4},{"alcohol":11.3},{"alcohol":11.2},{"alcohol":10.9},{"alcohol":9.2},{"alcohol":10.5},{"alcohol":8.8},{"alcohol":10.8},{"alcohol":9.8},{"alcohol":10.6},{"alcohol":9.4},{"alcohol":9.1},{"alcohol":10.2},{"alcohol":12.0},{"alcohol":12.0},{"alcohol":12.2},{"alcohol":13.3},{"alcohol":12.0},{"alcohol":12.7},{"alcohol":10.1},{"alcohol":9.3},{"alcohol":9.8},{"alcohol":9.4},{"alcohol":12.3},{"alcohol":12.1},{"alcohol":12.5},{"alcohol":9.1},{"alcohol":11.6},{"alcohol":10.4},{"alcohol":10.6},{"alcohol":13.0},{"alcohol":11.5},{"alcohol":10.5},{"alcohol":10.2},{"alcohol":9.8},{"alcohol":10.1},{"alcohol":11.2},{"alcohol":11.3},{"alcohol":12.4},{"alcohol":12.7},{"alcohol":10.2},{"alcohol":12.5},{"alcohol":10.7},{"alcohol":9.4},{"alcohol":10.8},{"alcohol":9.8},{"alcohol":10.3},{"alcohol":9.5},{"alcohol":9.5},{"alcohol":9.6},{"alcohol":9.0},{"alcohol":9.8},{"alcohol":9.7},{"alcohol":12.0},{"alcohol":10.1},{"alcohol":9.7},{"alcohol":12.4},{"alcohol":8.8},{"alcohol":12.5},{"alcohol":10.5},{"alcohol":9.7},{"alcohol":9.0},{"alcohol":8.7},{"alcohol":10.0},{"alcohol":12.2},{"alcohol":9.1},{"alcohol":9.9},{"alcohol":9.2},{"alcohol":9.0},{"alcohol":10.8},{"alcohol":11.0},{"alcohol":9.4},{"alcohol":11.3},{"alcohol":9.0},{"alcohol":12.0},{"alcohol":9.3},{"alcohol":10.8},{"alcohol":10.3},{"alcohol":13.4},{"alcohol":9.2},{"alcohol":12.2},{"alcohol":8.8},{"alcohol":9.8},{"alcohol":12.3},{"alcohol":11.1},{"alcohol":9.5},{"alcohol":9.3},{"alcohol":11.3},{"alcohol":10.4},{"alcohol":9.1},{"alcohol":9.7},{"alcohol":9.1},{"alcohol":10.3},{"alcohol":11.8},{"alcohol":9.9},{"alcohol":11.3},{"alcohol":11.4},{"alcohol":9.4},{"alcohol":9.6},{"alcohol":9.5},{"alcohol":10.8},{"alcohol":9.5},{"alcohol":10.4},{"alcohol":9.2},{"alcohol":9.1},{"alcohol":9.9},{"alcohol":12.7},{"alcohol":10.4},{"alcohol":9.4},{"alcohol":8.8},{"alcohol":10.6},{"alcohol":10.7},{"alcohol":8.8},{"alcohol":10.2},{"alcohol":9.1},{"alcohol":11.7},{"alcohol":9.2},{"alcohol":11.75},{"alcohol":9.5},{"alcohol":10.6},{"alcohol":11.1},{"alcohol":13.6},{"alcohol":11.8},{"alcohol":11.4},{"alcohol":12.3},{"alcohol":10.1},{"alcohol":9.4},{"alcohol":12.7},{"alcohol":11.1},{"alcohol":11.1},{"alcohol":10.3},{"alcohol":9.5},{"alcohol":11.4},{"alcohol":9.5},{"alcohol":9.7},{"alcohol":9.2},{"alcohol":9.3},{"alcohol":9.4},{"alcohol":9.5},{"alcohol":10.9},{"alcohol":13.0},{"alcohol":13.5},{"alcohol":9.9},{"alcohol":10.7},{"alcohol":9.5},{"alcohol":10.0},{"alcohol":10.6},{"alcohol":12.5},{"alcohol":10.6},{"alcohol":10.0},{"alcohol":12.5},{"alcohol":10.3},{"alcohol":9.8},{"alcohol":13.0},{"alcohol":9.4},{"alcohol":10.8},{"alcohol":12.8},{"alcohol":8.8},{"alcohol":9.2},{"alcohol":9.2},{"alcohol":9.6},{"alcohol":13.0},{"alcohol":12.9},{"alcohol":10.4},{"alcohol":11.5},{"alcohol":11.7},{"alcohol":10.9666666666667},{"alcohol":8.9},{"alcohol":12.3},{"alcohol":9.7},{"alcohol":10.1},{"alcohol":8.8},{"alcohol":9.2},{"alcohol":11.0},{"alcohol":10.5},{"alcohol":10.0},{"alcohol":11.7},{"alcohol":12.5},{"alcohol":12.9},{"alcohol":10.5},{"alcohol":9.6},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":8.4},{"alcohol":10.9},{"alcohol":10.4},{"alcohol":11.6},{"alcohol":12.4},{"alcohol":10.1},{"alcohol":9.1},{"alcohol":11.8},{"alcohol":11.0},{"alcohol":9.7},{"alcohol":10.1},{"alcohol":11.2},{"alcohol":9.2},{"alcohol":9.5},{"alcohol":12.3},{"alcohol":9.0},{"alcohol":10.6},{"alcohol":11.94},{"alcohol":9.8},{"alcohol":9.2},{"alcohol":10.3},{"alcohol":8.9},{"alcohol":10.2},{"alcohol":9.1},{"alcohol":9.9},{"alcohol":11.4},{"alcohol":11.2},{"alcohol":12.5},{"alcohol":11.0},{"alcohol":9.9},{"alcohol":10.6},{"alcohol":10.2},{"alcohol":9.4},{"alcohol":10.7},{"alcohol":11.6},{"alcohol":10.4},{"alcohol":11.7},{"alcohol":11.2},{"alcohol":11.4},{"alcohol":8.0},{"alcohol":10.8},{"alcohol":9.0},{"alcohol":10.3},{"alcohol":10.2},{"alcohol":9.8},{"alcohol":9.2},{"alcohol":9.8},{"alcohol":9.9},{"alcohol":8.9},{"alcohol":8.9},{"alcohol":10.2},{"alcohol":11.8},{"alcohol":10.5},{"alcohol":9.4},{"alcohol":12.7},{"alcohol":12.0},{"alcohol":13.0},{"alcohol":9.3},{"alcohol":9.0},{"alcohol":8.7},{"alcohol":10.6},{"alcohol":12.0},{"alcohol":9.4},{"alcohol":9.0},{"alcohol":11.0},{"alcohol":11.8},{"alcohol":8.9},{"alcohol":10.1},{"alcohol":9.9},{"alcohol":11.0},{"alcohol":11.0},{"alcohol":10.4},{"alcohol":10.4},{"alcohol":12.8},{"alcohol":10.0},{"alcohol":11.4},{"alcohol":9.2},{"alcohol":8.7},{"alcohol":9.5},{"alcohol":9.8},{"alcohol":9.9},{"alcohol":9.9},{"alcohol":12.4},{"alcohol":9.9},{"alcohol":10.9},{"alcohol":11.0},{"alcohol":11.4},{"alcohol":9.8},{"alcohol":9.9}]},"encoding":{"x":{"axis":{"title":"% of alcohol"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"lightblue","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":"KDE plot of alcohol feature"},"transform":[{"counts":false,"cumulative":false,"density":"alcohol","maxsteps":200,"minsteps":25}],"width":350},{"data":{"values":[{"pH":3.37},{"pH":3.23},{"pH":2.99},{"pH":3.28},{"pH":3.3},{"pH":3.16},{"pH":3.14},{"pH":3.16},{"pH":2.99},{"pH":3.25},{"pH":3.08},{"pH":2.99},{"pH":3.1},{"pH":2.97},{"pH":3.14},{"pH":3.13},{"pH":3.26},{"pH":3.09},{"pH":3.14},{"pH":3.31},{"pH":3.08},{"pH":3.2},{"pH":3.12},{"pH":3.05},{"pH":3.12},{"pH":3.29},{"pH":3.34},{"pH":2.97},{"pH":3.12},{"pH":3.34},{"pH":2.92},{"pH":3.12},{"pH":3.12},{"pH":3.15},{"pH":3.28},{"pH":3.37},{"pH":3.25},{"pH":3.16},{"pH":3.36},{"pH":3.22},{"pH":3.14},{"pH":3.16},{"pH":3.12},{"pH":3.18},{"pH":3.06},{"pH":3.14},{"pH":3.1},{"pH":3.17},{"pH":3.4},{"pH":3.14},{"pH":3.2},{"pH":2.88},{"pH":3.18},{"pH":3.19},{"pH":3.14},{"pH":3.38},{"pH":3.1},{"pH":3.08},{"pH":3.52},{"pH":3.33},{"pH":3.54},{"pH":3.0},{"pH":3.77},{"pH":3.2},{"pH":3.24},{"pH":3.3},{"pH":3.32},{"pH":3.15},{"pH":3.12},{"pH":3.59},{"pH":3.18},{"pH":2.96},{"pH":3.16},{"pH":3.11},{"pH":3.42},{"pH":3.25},{"pH":3.1},{"pH":3.23},{"pH":3.34},{"pH":3.12},{"pH":3.48},{"pH":3.29},{"pH":3.12},{"pH":3.02},{"pH":2.99},{"pH":3.32},{"pH":3.29},{"pH":3.19},{"pH":3.09},{"pH":3.12},{"pH":3.14},{"pH":3.16},{"pH":3.26},{"pH":3.04},{"pH":3.08},{"pH":3.07},{"pH":2.98},{"pH":3.2},{"pH":3.45},{"pH":3.27},{"pH":3.29},{"pH":3.1},{"pH":3.25},{"pH":2.99},{"pH":3.22},{"pH":3.19},{"pH":3.27},{"pH":3.18},{"pH":3.19},{"pH":3.14},{"pH":3.13},{"pH":3.14},{"pH":3.26},{"pH":3.24},{"pH":3.16},{"pH":3.11},{"pH":3.44},{"pH":3.33},{"pH":3.2},{"pH":3.14},{"pH":3.21},{"pH":3.15},{"pH":3.2},{"pH":3.13},{"pH":3.31},{"pH":3.2},{"pH":3.02},{"pH":3.14},{"pH":3.08},{"pH":3.25},{"pH":3.12},{"pH":2.86},{"pH":3.17},{"pH":3.18},{"pH":3.43},{"pH":3.12},{"pH":3.16},{"pH":3.08},{"pH":3.28},{"pH":3.32},{"pH":3.22},{"pH":3.26},{"pH":3.07},{"pH":3.06},{"pH":3.31},{"pH":3.23},{"pH":3.3},{"pH":3.54},{"pH":3.0},{"pH":3.22},{"pH":3.16},{"pH":2.95},{"pH":3.32},{"pH":3.27},{"pH":3.44},{"pH":3.02},{"pH":3.41},{"pH":3.19},{"pH":3.36},{"pH":3.26},{"pH":3.09},{"pH":3.15},{"pH":3.08},{"pH":3.27},{"pH":3.3},{"pH":3.07},{"pH":3.15},{"pH":3.19},{"pH":3.07},{"pH":3.26},{"pH":3.5},{"pH":2.96},{"pH":3.22},{"pH":3.14},{"pH":3.34},{"pH":3.06},{"pH":3.43},{"pH":3.04},{"pH":3.19},{"pH":3.08},{"pH":3.16},{"pH":3.04},{"pH":2.93},{"pH":3.12},{"pH":3.09},{"pH":3.35},{"pH":3.15},{"pH":3.29},{"pH":3.04},{"pH":3.1},{"pH":3.11},{"pH":3.07},{"pH":3.34},{"pH":3.11},{"pH":3.2},{"pH":3.16},{"pH":3.74},{"pH":3.3},{"pH":3.18},{"pH":3.4},{"pH":3.21},{"pH":3.15},{"pH":2.99},{"pH":2.86},{"pH":3.19},{"pH":3.13},{"pH":3.46},{"pH":3.27},{"pH":3.32},{"pH":3.3},{"pH":3.14},{"pH":3.46},{"pH":3.18},{"pH":2.85},{"pH":3.08},{"pH":3.29},{"pH":3.26},{"pH":2.97},{"pH":3.33},{"pH":3.0},{"pH":3.05},{"pH":3.16},{"pH":2.94},{"pH":3.47},{"pH":3.11},{"pH":3.14},{"pH":3.55},{"pH":2.98},{"pH":3.36},{"pH":3.12},{"pH":3.18},{"pH":2.98},{"pH":2.95},{"pH":3.19},{"pH":3.07},{"pH":3.11},{"pH":3.11},{"pH":3.2},{"pH":3.07},{"pH":3.38},{"pH":3.18},{"pH":3.2},{"pH":3.44},{"pH":3.21},{"pH":3.3},{"pH":2.98},{"pH":3.23},{"pH":3.23},{"pH":3.45},{"pH":2.95},{"pH":3.23},{"pH":3.21},{"pH":3.02},{"pH":3.15},{"pH":3.21},{"pH":3.12},{"pH":3.23},{"pH":3.1},{"pH":3.31},{"pH":3.16},{"pH":3.18},{"pH":3.24},{"pH":3.14},{"pH":3.51},{"pH":3.29},{"pH":3.3},{"pH":2.96},{"pH":3.13},{"pH":3.14},{"pH":3.06},{"pH":3.18},{"pH":3.46},{"pH":3.14},{"pH":3.11},{"pH":3.1},{"pH":3.11},{"pH":3.17},{"pH":3.09},{"pH":3.38},{"pH":3.15},{"pH":3.38},{"pH":3.29},{"pH":3.32},{"pH":3.1},{"pH":3.03},{"pH":2.93},{"pH":3.25},{"pH":3.25},{"pH":3.34},{"pH":3.12},{"pH":3.36},{"pH":3.15},{"pH":3.12},{"pH":3.1},{"pH":3.24},{"pH":2.87},{"pH":2.93},{"pH":3.12},{"pH":3.15},{"pH":3.31},{"pH":3.14},{"pH":3.31},{"pH":3.29},{"pH":3.42},{"pH":3.15},{"pH":3.09},{"pH":2.96},{"pH":3.04},{"pH":3.25},{"pH":3.1},{"pH":3.34},{"pH":3.22},{"pH":3.28},{"pH":3.26},{"pH":3.01},{"pH":3.16},{"pH":3.25},{"pH":3.19},{"pH":3.22},{"pH":3.18},{"pH":3.23},{"pH":3.23},{"pH":3.07},{"pH":3.09},{"pH":3.08},{"pH":3.39},{"pH":3.34},{"pH":2.98},{"pH":3.45},{"pH":2.9},{"pH":3.46},{"pH":3.21},{"pH":3.09},{"pH":3.13},{"pH":3.42},{"pH":3.15},{"pH":3.14},{"pH":3.12},{"pH":3.22},{"pH":3.3},{"pH":3.15},{"pH":3.14},{"pH":3.5},{"pH":3.24},{"pH":3.27},{"pH":3.34},{"pH":3.34},{"pH":3.39},{"pH":3.36},{"pH":3.19},{"pH":3.15},{"pH":3.2},{"pH":2.93},{"pH":3.18},{"pH":3.08},{"pH":3.36},{"pH":3.07},{"pH":2.91},{"pH":2.97},{"pH":3.05},{"pH":3.06},{"pH":3.22},{"pH":3.08},{"pH":3.28},{"pH":3.19},{"pH":2.94},{"pH":3.21},{"pH":3.25},{"pH":3.21},{"pH":3.24},{"pH":3.08},{"pH":3.2},{"pH":2.96},{"pH":3.19},{"pH":3.44},{"pH":3.15},{"pH":2.91},{"pH":3.03},{"pH":3.22},{"pH":3.1},{"pH":3.14},{"pH":3.28},{"pH":3.25},{"pH":3.3},{"pH":3.12},{"pH":3.4},{"pH":3.1},{"pH":3.05},{"pH":3.15},{"pH":3.23},{"pH":3.09},{"pH":3.38},{"pH":3.39},{"pH":3.13},{"pH":3.06},{"pH":3.15},{"pH":3.51},{"pH":3.02},{"pH":3.17},{"pH":3.11},{"pH":3.41},{"pH":3.22},{"pH":3.34},{"pH":3.13},{"pH":3.25},{"pH":3.44},{"pH":3.08},{"pH":3.39},{"pH":3.33},{"pH":3.1},{"pH":3.0},{"pH":3.35},{"pH":3.3},{"pH":3.16},{"pH":2.99},{"pH":3.36},{"pH":3.15},{"pH":2.9},{"pH":3.41},{"pH":3.12},{"pH":3.08},{"pH":3.23},{"pH":3.26},{"pH":3.16},{"pH":3.14},{"pH":3.42},{"pH":3.24},{"pH":3.17},{"pH":3.47},{"pH":3.5},{"pH":3.28},{"pH":2.9},{"pH":3.26},{"pH":3.16},{"pH":3.12},{"pH":2.79},{"pH":3.04},{"pH":2.99},{"pH":3.26},{"pH":3.14},{"pH":3.3},{"pH":2.86},{"pH":3.09},{"pH":3.2},{"pH":3.36},{"pH":3.25},{"pH":3.09},{"pH":3.3},{"pH":3.41},{"pH":3.46},{"pH":3.28},{"pH":3.01},{"pH":2.88},{"pH":3.24},{"pH":3.22},{"pH":3.12},{"pH":3.28},{"pH":3.34},{"pH":3.38},{"pH":3.06},{"pH":3.08},{"pH":3.5},{"pH":3.12},{"pH":3.05},{"pH":3.06},{"pH":3.29},{"pH":3.06},{"pH":3.19},{"pH":3.16},{"pH":3.18},{"pH":3.13},{"pH":3.2},{"pH":3.46},{"pH":3.14},{"pH":3.02},{"pH":3.09},{"pH":3.09},{"pH":3.34},{"pH":3.13},{"pH":3.34},{"pH":3.16},{"pH":3.1},{"pH":3.0},{"pH":2.91},{"pH":3.1},{"pH":3.14},{"pH":3.16},{"pH":3.23},{"pH":3.26},{"pH":3.01},{"pH":3.29},{"pH":3.09},{"pH":3.28},{"pH":3.27},{"pH":3.27},{"pH":3.37},{"pH":2.96},{"pH":3.34},{"pH":3.16},{"pH":3.23},{"pH":3.4},{"pH":3.13},{"pH":2.99},{"pH":3.39},{"pH":3.34},{"pH":3.43},{"pH":3.23},{"pH":3.27},{"pH":3.63},{"pH":3.2},{"pH":3.19},{"pH":2.85},{"pH":3.25},{"pH":3.07},{"pH":3.16},{"pH":3.16},{"pH":3.17},{"pH":3.19},{"pH":3.53},{"pH":3.11},{"pH":3.24},{"pH":3.58},{"pH":3.14},{"pH":3.16},{"pH":2.95},{"pH":3.16},{"pH":3.29},{"pH":3.16},{"pH":3.49},{"pH":3.11},{"pH":3.0},{"pH":3.39},{"pH":3.37},{"pH":2.96},{"pH":3.1},{"pH":3.36},{"pH":3.12},{"pH":2.99},{"pH":3.08},{"pH":3.16},{"pH":3.31},{"pH":3.07},{"pH":3.31},{"pH":3.04},{"pH":3.08},{"pH":3.2},{"pH":3.1},{"pH":3.23},{"pH":3.18},{"pH":3.21},{"pH":3.08},{"pH":3.15},{"pH":3.34},{"pH":3.05},{"pH":2.92},{"pH":3.0},{"pH":3.31},{"pH":3.15},{"pH":3.16},{"pH":3.3},{"pH":3.53},{"pH":3.16},{"pH":3.02},{"pH":3.21},{"pH":3.51},{"pH":3.22},{"pH":3.19},{"pH":2.93},{"pH":3.1},{"pH":3.08},{"pH":3.22},{"pH":3.13},{"pH":3.05},{"pH":3.04},{"pH":2.95},{"pH":3.03},{"pH":3.3},{"pH":3.2},{"pH":3.55},{"pH":3.19},{"pH":3.26},{"pH":3.41},{"pH":3.04},{"pH":3.07},{"pH":3.34},{"pH":3.21},{"pH":3.2},{"pH":3.16},{"pH":3.25},{"pH":3.05},{"pH":3.21},{"pH":3.12},{"pH":3.06},{"pH":3.03},{"pH":3.24},{"pH":3.15},{"pH":3.37},{"pH":3.46},{"pH":3.15},{"pH":3.2},{"pH":3.41},{"pH":3.51},{"pH":3.19},{"pH":3.5},{"pH":3.3},{"pH":3.05},{"pH":3.36},{"pH":3.2},{"pH":3.51},{"pH":3.22},{"pH":3.09},{"pH":3.25},{"pH":3.34},{"pH":2.88},{"pH":3.24},{"pH":3.2},{"pH":3.16},{"pH":3.11},{"pH":3.13},{"pH":3.3},{"pH":3.14},{"pH":3.24},{"pH":3.13},{"pH":3.07},{"pH":3.18},{"pH":2.99},{"pH":3.09},{"pH":2.99},{"pH":3.18},{"pH":3.32},{"pH":3.31},{"pH":3.04},{"pH":3.41},{"pH":3.24},{"pH":3.23},{"pH":3.15},{"pH":3.2},{"pH":2.89},{"pH":3.27},{"pH":3.2},{"pH":2.91},{"pH":3.51},{"pH":3.37},{"pH":3.09},{"pH":3.21},{"pH":3.03},{"pH":3.06},{"pH":3.11},{"pH":3.16},{"pH":3.14},{"pH":3.19},{"pH":3.15},{"pH":3.34},{"pH":2.99},{"pH":3.23},{"pH":3.06},{"pH":3.1},{"pH":3.16},{"pH":3.14},{"pH":3.11},{"pH":2.99},{"pH":3.14},{"pH":3.12},{"pH":3.0},{"pH":3.35},{"pH":3.24},{"pH":3.17},{"pH":3.13},{"pH":3.39},{"pH":3.2},{"pH":3.28},{"pH":3.42},{"pH":3.03},{"pH":3.04},{"pH":3.1},{"pH":3.08},{"pH":3.24},{"pH":3.12},{"pH":3.4},{"pH":3.35},{"pH":3.19},{"pH":3.06},{"pH":3.24},{"pH":3.1},{"pH":3.02},{"pH":3.06},{"pH":3.66},{"pH":3.12},{"pH":3.23},{"pH":3.26},{"pH":3.05},{"pH":2.93},{"pH":3.16},{"pH":3.0},{"pH":3.31},{"pH":3.01},{"pH":3.23},{"pH":3.29},{"pH":3.38},{"pH":3.35},{"pH":3.2},{"pH":3.0},{"pH":3.24},{"pH":3.05},{"pH":3.35},{"pH":3.15},{"pH":3.22},{"pH":3.14},{"pH":3.2},{"pH":3.3},{"pH":3.27},{"pH":3.28},{"pH":3.14},{"pH":3.12},{"pH":3.18},{"pH":3.17},{"pH":3.24},{"pH":3.2},{"pH":3.32},{"pH":3.47},{"pH":3.36},{"pH":3.42},{"pH":3.18},{"pH":3.36},{"pH":3.15},{"pH":3.1},{"pH":3.39},{"pH":3.11},{"pH":3.21},{"pH":3.48},{"pH":3.38},{"pH":3.12},{"pH":3.31},{"pH":3.39},{"pH":3.18},{"pH":3.28},{"pH":3.32},{"pH":3.19},{"pH":3.06},{"pH":2.96},{"pH":3.41},{"pH":3.02},{"pH":3.51},{"pH":3.14},{"pH":3.12},{"pH":3.13},{"pH":3.49},{"pH":3.27},{"pH":3.34},{"pH":3.23},{"pH":3.35},{"pH":3.24},{"pH":2.89},{"pH":3.47},{"pH":3.75},{"pH":3.21},{"pH":3.19},{"pH":3.08},{"pH":3.08},{"pH":3.21},{"pH":3.32},{"pH":3.15},{"pH":3.38},{"pH":3.17},{"pH":3.17},{"pH":3.1},{"pH":3.25},{"pH":3.13},{"pH":3.49},{"pH":3.15},{"pH":3.25},{"pH":3.12},{"pH":3.02},{"pH":3.3},{"pH":3.17},{"pH":3.22},{"pH":3.16},{"pH":3.24},{"pH":3.33},{"pH":3.21},{"pH":2.99},{"pH":3.07},{"pH":3.3},{"pH":3.11},{"pH":3.19},{"pH":3.08},{"pH":3.22},{"pH":3.2},{"pH":3.04},{"pH":2.84},{"pH":3.39},{"pH":3.14},{"pH":3.2},{"pH":3.08},{"pH":3.12},{"pH":2.9},{"pH":3.34},{"pH":3.17},{"pH":3.16},{"pH":3.06},{"pH":2.89},{"pH":3.32},{"pH":2.98},{"pH":3.11},{"pH":3.16},{"pH":3.2},{"pH":3.12},{"pH":3.38},{"pH":3.12},{"pH":3.26},{"pH":3.3},{"pH":3.25},{"pH":3.37},{"pH":3.03},{"pH":3.09},{"pH":2.97},{"pH":3.34},{"pH":3.05},{"pH":3.45},{"pH":3.28},{"pH":3.08},{"pH":3.13},{"pH":3.12},{"pH":2.96},{"pH":3.14},{"pH":3.5},{"pH":3.41},{"pH":3.24},{"pH":3.09},{"pH":3.27},{"pH":3.47},{"pH":3.26},{"pH":3.37},{"pH":3.15},{"pH":3.14},{"pH":3.13},{"pH":2.99},{"pH":3.11},{"pH":3.13},{"pH":2.98},{"pH":3.29},{"pH":3.18},{"pH":2.94},{"pH":3.27},{"pH":3.07},{"pH":3.03},{"pH":2.97},{"pH":3.18},{"pH":3.53},{"pH":3.38},{"pH":3.14},{"pH":3.29},{"pH":3.27},{"pH":3.39},{"pH":3.17},{"pH":3.08},{"pH":3.11},{"pH":3.16},{"pH":3.26},{"pH":3.25},{"pH":3.29},{"pH":3.3},{"pH":3.23},{"pH":3.36},{"pH":3.29},{"pH":3.05},{"pH":3.25},{"pH":3.3},{"pH":3.12},{"pH":3.25},{"pH":3.33},{"pH":3.36},{"pH":3.36},{"pH":3.24},{"pH":3.28},{"pH":3.14},{"pH":3.12},{"pH":3.31},{"pH":3.16},{"pH":3.05},{"pH":3.31},{"pH":3.34},{"pH":3.06},{"pH":3.19},{"pH":3.13},{"pH":3.29},{"pH":3.19},{"pH":3.18},{"pH":3.33},{"pH":3.27},{"pH":3.22},{"pH":3.19},{"pH":3.32},{"pH":3.26},{"pH":3.15},{"pH":2.94},{"pH":2.86},{"pH":3.08},{"pH":3.03},{"pH":2.93},{"pH":3.42},{"pH":3.37},{"pH":3.16},{"pH":3.17},{"pH":3.06},{"pH":3.25},{"pH":2.96},{"pH":2.98},{"pH":3.25},{"pH":2.99},{"pH":3.01},{"pH":3.06},{"pH":3.15},{"pH":3.31},{"pH":3.01},{"pH":3.37},{"pH":3.28},{"pH":2.89},{"pH":2.99},{"pH":3.22},{"pH":3.2},{"pH":3.22},{"pH":3.19},{"pH":3.11},{"pH":3.56},{"pH":3.4},{"pH":3.22},{"pH":3.26},{"pH":3.31},{"pH":3.21},{"pH":2.96},{"pH":3.15},{"pH":3.27},{"pH":3.3},{"pH":3.01},{"pH":3.2},{"pH":3.0},{"pH":3.18},{"pH":3.13},{"pH":3.06},{"pH":3.03},{"pH":3.42},{"pH":3.25},{"pH":3.06},{"pH":3.0},{"pH":3.15},{"pH":3.42},{"pH":3.02},{"pH":3.27},{"pH":3.54},{"pH":3.09},{"pH":3.4},{"pH":3.17},{"pH":3.27},{"pH":3.26},{"pH":3.18},{"pH":3.24},{"pH":3.43},{"pH":3.35},{"pH":3.42},{"pH":3.04},{"pH":3.36},{"pH":3.39},{"pH":3.58},{"pH":3.31},{"pH":3.15},{"pH":3.13},{"pH":3.04},{"pH":3.31},{"pH":3.05},{"pH":3.04},{"pH":3.17},{"pH":3.29},{"pH":2.87},{"pH":3.27},{"pH":3.11},{"pH":3.42},{"pH":3.06},{"pH":3.28},{"pH":3.3},{"pH":3.4},{"pH":3.18},{"pH":3.23},{"pH":3.13},{"pH":3.21},{"pH":3.1},{"pH":2.97},{"pH":3.22},{"pH":3.34},{"pH":3.13},{"pH":3.21},{"pH":3.21},{"pH":3.29},{"pH":3.35},{"pH":3.47},{"pH":2.97},{"pH":3.17},{"pH":3.09},{"pH":3.1},{"pH":2.98},{"pH":3.13},{"pH":3.23},{"pH":2.92},{"pH":3.08},{"pH":3.08},{"pH":3.25},{"pH":3.22},{"pH":3.04},{"pH":2.9},{"pH":3.29},{"pH":3.76},{"pH":3.41},{"pH":2.99},{"pH":3.2},{"pH":3.09},{"pH":3.06},{"pH":3.36},{"pH":3.45},{"pH":3.04},{"pH":3.2},{"pH":3.25},{"pH":3.34},{"pH":3.17},{"pH":3.15},{"pH":3.08},{"pH":3.32},{"pH":3.3},{"pH":3.23},{"pH":3.24},{"pH":3.24},{"pH":3.42},{"pH":3.02},{"pH":2.96},{"pH":3.11},{"pH":3.24},{"pH":3.13},{"pH":3.23},{"pH":3.22},{"pH":3.25},{"pH":3.35},{"pH":3.36},{"pH":3.32},{"pH":3.17},{"pH":3.26},{"pH":3.31},{"pH":3.26},{"pH":2.93},{"pH":3.03},{"pH":3.35},{"pH":3.24},{"pH":3.05},{"pH":3.23},{"pH":3.13},{"pH":3.37},{"pH":3.56},{"pH":3.23},{"pH":3.09},{"pH":3.36},{"pH":3.23},{"pH":3.36},{"pH":3.29},{"pH":3.04},{"pH":3.06},{"pH":3.58},{"pH":3.1},{"pH":3.03},{"pH":3.21},{"pH":3.12},{"pH":3.24},{"pH":3.08},{"pH":3.16},{"pH":3.12},{"pH":3.32},{"pH":3.3},{"pH":3.3},{"pH":3.02},{"pH":3.15},{"pH":3.39},{"pH":3.37},{"pH":3.19},{"pH":3.1},{"pH":3.36},{"pH":3.16},{"pH":2.91},{"pH":3.1},{"pH":3.19},{"pH":3.05},{"pH":3.37},{"pH":3.21},{"pH":3.28},{"pH":3.08},{"pH":2.99},{"pH":3.33},{"pH":3.19},{"pH":3.17},{"pH":3.14},{"pH":3.25},{"pH":3.29},{"pH":2.99},{"pH":3.18},{"pH":3.39},{"pH":3.4},{"pH":3.49},{"pH":3.32},{"pH":3.13},{"pH":3.12},{"pH":3.12},{"pH":2.95},{"pH":3.27},{"pH":3.16},{"pH":3.32},{"pH":3.1},{"pH":3.54},{"pH":2.9},{"pH":3.07},{"pH":3.39},{"pH":3.09},{"pH":3.14},{"pH":3.08},{"pH":3.19},{"pH":3.19},{"pH":3.39},{"pH":3.25},{"pH":3.29},{"pH":3.13},{"pH":3.2},{"pH":2.92},{"pH":3.29},{"pH":3.22},{"pH":3.27},{"pH":3.09},{"pH":3.4},{"pH":3.16},{"pH":3.24},{"pH":3.22},{"pH":3.19},{"pH":3.08},{"pH":3.11},{"pH":3.34},{"pH":3.09},{"pH":3.03},{"pH":3.27},{"pH":3.25},{"pH":3.13},{"pH":3.08},{"pH":3.16},{"pH":3.43},{"pH":3.43},{"pH":3.12},{"pH":3.16},{"pH":3.27},{"pH":3.09},{"pH":3.42},{"pH":3.26},{"pH":3.2},{"pH":2.98},{"pH":3.11},{"pH":2.9},{"pH":2.93},{"pH":3.38},{"pH":3.34},{"pH":3.27},{"pH":3.48},{"pH":3.1},{"pH":3.1},{"pH":3.13},{"pH":2.99},{"pH":3.55},{"pH":3.13},{"pH":3.09},{"pH":2.9},{"pH":2.99},{"pH":3.03},{"pH":3.47},{"pH":3.23},{"pH":3.4},{"pH":3.26},{"pH":3.18},{"pH":3.39},{"pH":3.23},{"pH":3.04},{"pH":3.01},{"pH":2.93},{"pH":3.27},{"pH":3.26},{"pH":3.31},{"pH":3.36},{"pH":3.32},{"pH":3.32},{"pH":3.21},{"pH":3.23},{"pH":3.25},{"pH":3.18},{"pH":3.29},{"pH":2.79},{"pH":3.02},{"pH":3.31},{"pH":3.33},{"pH":3.01},{"pH":3.29},{"pH":3.31},{"pH":3.08},{"pH":3.23},{"pH":2.94},{"pH":3.01},{"pH":3.1},{"pH":3.43},{"pH":3.11},{"pH":3.15},{"pH":3.09},{"pH":3.29},{"pH":3.23},{"pH":3.46},{"pH":3.22},{"pH":3.2},{"pH":3.36},{"pH":3.35},{"pH":3.22},{"pH":3.29},{"pH":3.22},{"pH":3.21},{"pH":3.03},{"pH":2.88},{"pH":3.17},{"pH":3.17},{"pH":3.12},{"pH":3.2},{"pH":3.41},{"pH":3.3},{"pH":2.89},{"pH":3.09},{"pH":3.36},{"pH":3.06},{"pH":3.22},{"pH":3.16},{"pH":3.12},{"pH":3.3},{"pH":3.22},{"pH":3.01},{"pH":3.11},{"pH":3.16},{"pH":3.13},{"pH":3.12},{"pH":3.16},{"pH":3.19},{"pH":2.95},{"pH":3.34},{"pH":3.25},{"pH":3.0},{"pH":3.23},{"pH":3.07},{"pH":3.47},{"pH":3.26},{"pH":3.27},{"pH":3.15},{"pH":2.89},{"pH":2.96},{"pH":3.69},{"pH":3.18},{"pH":3.11},{"pH":3.22},{"pH":3.16},{"pH":3.16},{"pH":3.31},{"pH":3.05},{"pH":3.08},{"pH":3.08},{"pH":3.0},{"pH":3.17},{"pH":3.27},{"pH":3.22},{"pH":3.04},{"pH":3.09},{"pH":2.99},{"pH":3.22},{"pH":3.16},{"pH":3.26},{"pH":3.15},{"pH":3.29},{"pH":3.27},{"pH":3.02},{"pH":3.17},{"pH":3.32},{"pH":3.13},{"pH":3.4},{"pH":3.6},{"pH":3.1},{"pH":3.19},{"pH":3.21},{"pH":3.14},{"pH":3.16},{"pH":3.17},{"pH":3.31},{"pH":2.98},{"pH":3.36},{"pH":3.35},{"pH":3.13},{"pH":3.3},{"pH":3.35},{"pH":3.06},{"pH":3.31},{"pH":3.04},{"pH":3.18},{"pH":2.96},{"pH":3.05},{"pH":3.42},{"pH":3.16},{"pH":3.23},{"pH":3.42},{"pH":3.15},{"pH":2.9},{"pH":3.11},{"pH":3.28},{"pH":3.15},{"pH":3.32},{"pH":3.24},{"pH":3.0},{"pH":3.44},{"pH":3.08},{"pH":3.3},{"pH":3.2},{"pH":3.1},{"pH":3.21},{"pH":3.14},{"pH":3.23},{"pH":3.27},{"pH":3.14},{"pH":3.15},{"pH":3.24},{"pH":3.04},{"pH":3.25},{"pH":3.29},{"pH":3.52},{"pH":3.07},{"pH":3.18},{"pH":3.32},{"pH":3.17},{"pH":3.16},{"pH":3.61},{"pH":3.02},{"pH":3.0},{"pH":3.33},{"pH":3.48},{"pH":3.05},{"pH":3.22},{"pH":3.03},{"pH":3.28},{"pH":3.13},{"pH":3.03},{"pH":3.06},{"pH":3.19},{"pH":3.19},{"pH":3.13},{"pH":3.5},{"pH":3.31},{"pH":3.23},{"pH":3.33},{"pH":3.26},{"pH":3.21},{"pH":3.68},{"pH":3.17},{"pH":3.0},{"pH":3.25},{"pH":3.09},{"pH":3.21},{"pH":3.49},{"pH":3.11},{"pH":3.01},{"pH":3.07},{"pH":3.17},{"pH":3.02},{"pH":3.35},{"pH":3.19},{"pH":3.22},{"pH":3.26},{"pH":3.29},{"pH":3.04},{"pH":3.27},{"pH":3.22},{"pH":2.86},{"pH":3.19},{"pH":2.99},{"pH":3.21},{"pH":3.36},{"pH":3.2},{"pH":3.11},{"pH":2.89},{"pH":3.17},{"pH":3.12},{"pH":3.1},{"pH":3.49},{"pH":3.16},{"pH":3.25},{"pH":3.59},{"pH":3.27},{"pH":3.31},{"pH":2.95},{"pH":3.13},{"pH":3.12},{"pH":3.22},{"pH":3.07},{"pH":3.22},{"pH":3.18},{"pH":3.06},{"pH":3.08},{"pH":3.02},{"pH":3.0},{"pH":3.01},{"pH":3.08},{"pH":3.11},{"pH":3.06},{"pH":2.9},{"pH":3.2},{"pH":3.6},{"pH":3.11},{"pH":3.14},{"pH":3.1},{"pH":3.04},{"pH":3.48},{"pH":3.1},{"pH":3.4},{"pH":3.01},{"pH":3.39},{"pH":3.32},{"pH":3.15},{"pH":3.21},{"pH":3.24},{"pH":3.48},{"pH":3.13},{"pH":3.02},{"pH":3.21},{"pH":3.15},{"pH":3.03},{"pH":3.15},{"pH":3.11},{"pH":3.32},{"pH":3.09},{"pH":3.25},{"pH":3.51},{"pH":3.42},{"pH":3.14},{"pH":3.06},{"pH":3.1},{"pH":3.14},{"pH":3.18},{"pH":3.18},{"pH":3.01},{"pH":3.48},{"pH":3.3},{"pH":3.04},{"pH":3.54},{"pH":3.02},{"pH":3.31},{"pH":3.03},{"pH":3.22},{"pH":3.37},{"pH":3.0},{"pH":3.19},{"pH":3.2},{"pH":3.32},{"pH":3.14},{"pH":2.96},{"pH":3.16},{"pH":3.19},{"pH":3.33},{"pH":3.37},{"pH":3.04},{"pH":3.01},{"pH":3.15},{"pH":3.36},{"pH":3.38},{"pH":3.21},{"pH":3.28},{"pH":3.56},{"pH":3.31},{"pH":3.18},{"pH":3.06},{"pH":3.28},{"pH":3.0},{"pH":3.17},{"pH":3.35},{"pH":3.33},{"pH":3.2},{"pH":3.13},{"pH":2.97},{"pH":3.13},{"pH":3.31},{"pH":3.04},{"pH":3.19},{"pH":2.72},{"pH":3.18},{"pH":3.17},{"pH":3.23},{"pH":3.28},{"pH":3.1},{"pH":3.31},{"pH":3.1},{"pH":3.24},{"pH":3.22},{"pH":3.44},{"pH":2.88},{"pH":3.44},{"pH":3.01},{"pH":2.89},{"pH":3.2},{"pH":3.34},{"pH":3.23},{"pH":3.22},{"pH":3.01},{"pH":3.24},{"pH":3.04},{"pH":3.09},{"pH":3.03},{"pH":3.07},{"pH":3.14},{"pH":3.37},{"pH":3.2},{"pH":3.25},{"pH":3.13},{"pH":3.47},{"pH":3.29},{"pH":3.08},{"pH":3.15},{"pH":3.31},{"pH":3.24},{"pH":3.26},{"pH":3.11},{"pH":3.09},{"pH":3.34},{"pH":3.38},{"pH":3.2},{"pH":3.27},{"pH":3.1},{"pH":3.09},{"pH":3.25},{"pH":3.14},{"pH":3.25},{"pH":3.03},{"pH":3.53},{"pH":3.23},{"pH":3.12},{"pH":3.05},{"pH":3.19},{"pH":3.14},{"pH":3.33},{"pH":3.22},{"pH":3.06},{"pH":3.24},{"pH":3.07},{"pH":3.26},{"pH":3.27},{"pH":3.26},{"pH":3.04},{"pH":3.15},{"pH":2.83},{"pH":3.41},{"pH":3.12},{"pH":3.24},{"pH":3.02},{"pH":3.54},{"pH":3.35},{"pH":3.35},{"pH":3.12},{"pH":3.15},{"pH":3.62},{"pH":2.89},{"pH":3.13},{"pH":2.93},{"pH":3.65},{"pH":3.14},{"pH":3.07},{"pH":3.15},{"pH":3.16},{"pH":3.26},{"pH":2.98},{"pH":3.48},{"pH":3.08},{"pH":3.32},{"pH":3.24},{"pH":3.28},{"pH":3.23},{"pH":3.28},{"pH":3.46},{"pH":3.12},{"pH":3.17},{"pH":3.21},{"pH":3.16},{"pH":3.06},{"pH":3.23},{"pH":3.4},{"pH":3.42},{"pH":2.95},{"pH":3.16},{"pH":3.22},{"pH":3.3},{"pH":3.31},{"pH":3.22},{"pH":3.24},{"pH":3.13},{"pH":3.04},{"pH":3.26},{"pH":3.16},{"pH":3.19},{"pH":3.14},{"pH":3.1},{"pH":3.09},{"pH":3.32},{"pH":3.0},{"pH":3.0},{"pH":3.23},{"pH":3.14},{"pH":3.38},{"pH":2.93},{"pH":3.23},{"pH":3.26},{"pH":3.44},{"pH":3.0},{"pH":3.15},{"pH":3.11},{"pH":3.41},{"pH":2.96},{"pH":3.06},{"pH":3.27},{"pH":3.28},{"pH":3.13},{"pH":3.32},{"pH":3.41},{"pH":3.09},{"pH":3.08},{"pH":3.4},{"pH":3.34},{"pH":3.14},{"pH":2.94},{"pH":3.17},{"pH":3.19},{"pH":3.03},{"pH":3.0},{"pH":3.1},{"pH":3.02},{"pH":3.43},{"pH":2.98},{"pH":2.95},{"pH":3.14},{"pH":3.28},{"pH":3.22},{"pH":3.06},{"pH":3.13},{"pH":3.25},{"pH":3.25},{"pH":2.98},{"pH":3.21},{"pH":3.36},{"pH":3.32},{"pH":3.34},{"pH":3.06},{"pH":3.2},{"pH":2.93},{"pH":3.2},{"pH":3.3},{"pH":3.32},{"pH":3.17},{"pH":3.0},{"pH":3.44},{"pH":3.18},{"pH":3.19},{"pH":3.32},{"pH":3.09},{"pH":3.18},{"pH":3.06},{"pH":3.55},{"pH":3.13},{"pH":3.11},{"pH":3.0},{"pH":3.13},{"pH":3.18},{"pH":3.37},{"pH":3.14},{"pH":3.0},{"pH":3.15},{"pH":2.91},{"pH":3.3},{"pH":2.92},{"pH":3.25},{"pH":3.07},{"pH":3.32},{"pH":2.85},{"pH":3.18},{"pH":3.24},{"pH":3.05},{"pH":3.51},{"pH":3.02},{"pH":3.17},{"pH":3.22},{"pH":3.28},{"pH":3.15},{"pH":3.35},{"pH":3.29},{"pH":3.46},{"pH":2.97},{"pH":3.24},{"pH":3.26},{"pH":3.22},{"pH":3.1},{"pH":3.17},{"pH":3.04},{"pH":3.22},{"pH":3.05},{"pH":3.18},{"pH":2.97},{"pH":3.17},{"pH":3.17},{"pH":3.26},{"pH":3.35},{"pH":3.32},{"pH":3.33},{"pH":3.33},{"pH":2.98},{"pH":3.14},{"pH":3.24},{"pH":3.12},{"pH":3.13},{"pH":3.46},{"pH":3.12},{"pH":3.09},{"pH":3.22},{"pH":3.75},{"pH":2.98},{"pH":3.04},{"pH":2.98},{"pH":3.14},{"pH":3.26},{"pH":3.28},{"pH":3.17},{"pH":3.19},{"pH":3.41},{"pH":3.33},{"pH":3.18},{"pH":3.05},{"pH":3.08},{"pH":2.99},{"pH":3.36},{"pH":3.13},{"pH":3.25},{"pH":3.04},{"pH":3.18},{"pH":3.03},{"pH":3.18},{"pH":3.66},{"pH":3.08},{"pH":3.3},{"pH":3.17},{"pH":3.13},{"pH":3.25},{"pH":3.14},{"pH":3.22},{"pH":3.05},{"pH":3.4},{"pH":2.92},{"pH":3.13},{"pH":3.29},{"pH":3.05},{"pH":3.07},{"pH":3.21},{"pH":3.1},{"pH":3.27},{"pH":3.03},{"pH":3.22},{"pH":3.59},{"pH":3.2},{"pH":3.39},{"pH":3.34},{"pH":3.22},{"pH":3.26},{"pH":3.17},{"pH":3.06},{"pH":3.34},{"pH":3.37},{"pH":3.3},{"pH":3.27},{"pH":2.87},{"pH":3.21},{"pH":3.21},{"pH":2.77},{"pH":3.3},{"pH":3.33},{"pH":3.24},{"pH":3.21},{"pH":3.2},{"pH":3.41},{"pH":3.09},{"pH":3.08},{"pH":2.9},{"pH":3.1},{"pH":2.86},{"pH":3.06},{"pH":3.16},{"pH":3.29},{"pH":3.37},{"pH":2.96},{"pH":3.12},{"pH":3.19},{"pH":2.94},{"pH":3.66},{"pH":3.12},{"pH":3.05},{"pH":3.25},{"pH":3.16},{"pH":3.25},{"pH":3.14},{"pH":3.07},{"pH":2.97},{"pH":3.63},{"pH":3.09},{"pH":3.12},{"pH":3.18},{"pH":3.36},{"pH":3.37},{"pH":3.26},{"pH":3.55},{"pH":2.99},{"pH":3.57},{"pH":3.32},{"pH":3.3},{"pH":3.13},{"pH":2.98},{"pH":3.15},{"pH":2.93},{"pH":3.48},{"pH":3.05},{"pH":3.08},{"pH":3.08},{"pH":3.12},{"pH":3.1},{"pH":3.56},{"pH":3.1},{"pH":3.24},{"pH":3.24},{"pH":3.38},{"pH":3.25},{"pH":3.37},{"pH":3.0},{"pH":3.23},{"pH":2.99},{"pH":3.2},{"pH":3.17},{"pH":3.12},{"pH":3.21},{"pH":2.95},{"pH":3.04},{"pH":3.14},{"pH":3.27},{"pH":3.42},{"pH":3.24},{"pH":3.29},{"pH":3.14},{"pH":2.99},{"pH":3.1},{"pH":3.16},{"pH":3.27},{"pH":3.1},{"pH":3.18},{"pH":3.32},{"pH":3.29},{"pH":3.2},{"pH":3.18},{"pH":3.54},{"pH":3.06},{"pH":3.65},{"pH":3.24},{"pH":3.27},{"pH":3.35},{"pH":3.09},{"pH":3.01},{"pH":3.13},{"pH":3.06},{"pH":2.99},{"pH":3.09},{"pH":2.95},{"pH":3.16},{"pH":3.05},{"pH":3.16},{"pH":3.15},{"pH":3.23},{"pH":2.94},{"pH":3.23},{"pH":3.3},{"pH":3.4},{"pH":3.22},{"pH":3.05},{"pH":2.83},{"pH":3.07},{"pH":3.41},{"pH":3.16},{"pH":3.17},{"pH":2.93},{"pH":3.32},{"pH":3.31},{"pH":3.49},{"pH":3.16},{"pH":3.08},{"pH":3.05},{"pH":3.13},{"pH":3.01},{"pH":3.08},{"pH":3.22},{"pH":3.31},{"pH":3.35},{"pH":3.14},{"pH":3.12},{"pH":3.48},{"pH":3.21},{"pH":3.48},{"pH":3.23},{"pH":2.96},{"pH":3.31},{"pH":3.57},{"pH":3.19},{"pH":3.52},{"pH":3.16},{"pH":3.19},{"pH":3.13},{"pH":3.18},{"pH":3.01},{"pH":3.11},{"pH":3.44},{"pH":3.27},{"pH":3.23},{"pH":3.02},{"pH":3.18},{"pH":3.27},{"pH":2.93},{"pH":3.29},{"pH":3.1},{"pH":3.1},{"pH":3.27},{"pH":3.37},{"pH":3.44},{"pH":3.2},{"pH":2.97},{"pH":3.02},{"pH":3.08},{"pH":3.23},{"pH":2.95},{"pH":3.15},{"pH":3.13},{"pH":3.26},{"pH":2.96},{"pH":3.13},{"pH":3.3},{"pH":3.16},{"pH":3.21},{"pH":3.06},{"pH":3.14},{"pH":3.29},{"pH":3.3},{"pH":2.91},{"pH":3.14},{"pH":2.94},{"pH":3.14},{"pH":2.99},{"pH":3.12},{"pH":3.1},{"pH":3.18},{"pH":3.21},{"pH":3.2},{"pH":3.22},{"pH":3.38},{"pH":3.36},{"pH":3.16},{"pH":3.12},{"pH":3.06},{"pH":3.23},{"pH":3.11},{"pH":3.37},{"pH":3.42},{"pH":2.9},{"pH":3.09},{"pH":3.24},{"pH":2.93},{"pH":3.01},{"pH":3.08},{"pH":3.0},{"pH":3.36},{"pH":3.25},{"pH":3.28},{"pH":3.11},{"pH":3.1},{"pH":3.11},{"pH":3.24},{"pH":3.33},{"pH":3.27},{"pH":3.24},{"pH":3.15},{"pH":3.24},{"pH":3.01},{"pH":3.22},{"pH":3.17},{"pH":3.66},{"pH":3.01},{"pH":3.41},{"pH":2.93},{"pH":3.52},{"pH":3.14},{"pH":3.15},{"pH":3.38},{"pH":3.17},{"pH":3.12},{"pH":3.08},{"pH":3.39},{"pH":3.44},{"pH":3.17},{"pH":3.14},{"pH":3.21},{"pH":3.14},{"pH":3.05},{"pH":3.24},{"pH":3.27},{"pH":3.08},{"pH":3.0},{"pH":3.2},{"pH":3.14},{"pH":3.07},{"pH":3.28},{"pH":3.38},{"pH":3.1},{"pH":3.25},{"pH":3.3},{"pH":3.09},{"pH":3.18},{"pH":3.2},{"pH":3.11},{"pH":3.26},{"pH":3.2},{"pH":3.11},{"pH":3.32},{"pH":3.08},{"pH":3.18},{"pH":3.42},{"pH":3.39},{"pH":3.24},{"pH":3.36},{"pH":3.32},{"pH":3.17},{"pH":3.4},{"pH":3.29},{"pH":3.02},{"pH":3.2},{"pH":3.26},{"pH":3.2},{"pH":3.07},{"pH":3.06},{"pH":3.11},{"pH":2.96},{"pH":3.08},{"pH":3.3},{"pH":3.16},{"pH":3.08},{"pH":3.09},{"pH":3.16},{"pH":3.08},{"pH":3.47},{"pH":3.04},{"pH":3.02},{"pH":3.16},{"pH":3.22},{"pH":3.02},{"pH":3.37},{"pH":3.11},{"pH":3.57},{"pH":3.06},{"pH":3.44},{"pH":3.06},{"pH":3.44},{"pH":2.88},{"pH":3.07},{"pH":2.99},{"pH":3.0},{"pH":3.19},{"pH":3.06},{"pH":3.2},{"pH":3.32},{"pH":3.23},{"pH":3.03},{"pH":2.89},{"pH":3.19},{"pH":3.25},{"pH":3.24},{"pH":3.24},{"pH":3.12},{"pH":3.41},{"pH":3.19},{"pH":3.25},{"pH":3.0},{"pH":3.03},{"pH":3.28},{"pH":3.29},{"pH":3.35},{"pH":3.25},{"pH":3.38},{"pH":3.23},{"pH":3.04},{"pH":3.28},{"pH":3.15},{"pH":3.24},{"pH":3.26},{"pH":2.92},{"pH":3.37},{"pH":3.15},{"pH":3.04},{"pH":3.32},{"pH":3.14},{"pH":3.25},{"pH":3.19},{"pH":3.14},{"pH":3.07},{"pH":3.21},{"pH":3.12},{"pH":3.29},{"pH":3.28},{"pH":3.23},{"pH":3.26},{"pH":3.16},{"pH":3.22},{"pH":2.92},{"pH":3.03},{"pH":3.06},{"pH":3.05},{"pH":3.02},{"pH":3.22},{"pH":3.08},{"pH":3.36},{"pH":3.24},{"pH":3.39},{"pH":3.28},{"pH":3.05},{"pH":3.31},{"pH":3.39},{"pH":3.12},{"pH":3.23},{"pH":3.25},{"pH":3.18},{"pH":3.82},{"pH":3.22},{"pH":3.33},{"pH":3.23},{"pH":3.1},{"pH":3.44},{"pH":3.26},{"pH":3.33},{"pH":3.06},{"pH":3.08},{"pH":3.37},{"pH":2.99},{"pH":3.33},{"pH":3.07},{"pH":3.43},{"pH":3.06},{"pH":3.2},{"pH":3.1},{"pH":2.83},{"pH":3.13},{"pH":3.31},{"pH":3.42},{"pH":3.1},{"pH":3.02},{"pH":2.99},{"pH":3.04},{"pH":3.12},{"pH":3.13},{"pH":3.02},{"pH":3.12},{"pH":3.02},{"pH":3.24},{"pH":3.28},{"pH":3.17},{"pH":3.27},{"pH":3.46},{"pH":3.09},{"pH":3.17},{"pH":3.04},{"pH":2.96},{"pH":3.15},{"pH":3.19},{"pH":3.3},{"pH":3.24},{"pH":3.21},{"pH":3.11},{"pH":3.17},{"pH":3.05},{"pH":3.15},{"pH":3.06},{"pH":3.16},{"pH":3.12},{"pH":3.14},{"pH":3.13},{"pH":3.22},{"pH":3.13},{"pH":3.22},{"pH":3.07},{"pH":3.21},{"pH":2.99},{"pH":2.99},{"pH":3.24},{"pH":3.17},{"pH":3.31},{"pH":3.17},{"pH":3.08},{"pH":3.09},{"pH":3.2},{"pH":2.98},{"pH":3.11},{"pH":3.14},{"pH":3.19},{"pH":3.1},{"pH":3.11},{"pH":2.99},{"pH":3.28},{"pH":3.33},{"pH":3.32},{"pH":3.15},{"pH":3.28},{"pH":3.27},{"pH":3.17},{"pH":3.22},{"pH":3.16},{"pH":3.38},{"pH":3.08},{"pH":2.88},{"pH":3.1},{"pH":3.5},{"pH":3.08},{"pH":3.38},{"pH":3.52},{"pH":3.32},{"pH":3.23},{"pH":3.36},{"pH":3.19},{"pH":3.48},{"pH":3.2},{"pH":2.9},{"pH":3.12},{"pH":3.66},{"pH":2.98},{"pH":3.15},{"pH":3.11},{"pH":2.97},{"pH":2.99},{"pH":3.18},{"pH":2.94},{"pH":3.22},{"pH":3.2},{"pH":3.18},{"pH":3.19},{"pH":3.2},{"pH":3.23},{"pH":3.19},{"pH":3.23},{"pH":3.28},{"pH":3.3},{"pH":3.25},{"pH":3.15},{"pH":3.25},{"pH":3.06},{"pH":3.22},{"pH":3.12},{"pH":3.45},{"pH":3.26},{"pH":3.13},{"pH":3.05},{"pH":3.19},{"pH":3.03},{"pH":3.2},{"pH":3.14},{"pH":3.23},{"pH":3.17},{"pH":3.08},{"pH":3.19},{"pH":3.13},{"pH":3.09},{"pH":3.45},{"pH":3.42},{"pH":3.05},{"pH":3.19},{"pH":3.08},{"pH":3.32},{"pH":3.4},{"pH":3.28},{"pH":3.14},{"pH":3.33},{"pH":3.12},{"pH":3.2},{"pH":3.42},{"pH":3.27},{"pH":3.11},{"pH":3.31},{"pH":3.23},{"pH":3.25},{"pH":3.05},{"pH":3.17},{"pH":3.28},{"pH":3.21},{"pH":3.11},{"pH":2.79},{"pH":3.04},{"pH":3.27},{"pH":3.19},{"pH":3.3},{"pH":2.92},{"pH":3.24},{"pH":3.15},{"pH":3.2},{"pH":2.98},{"pH":3.23},{"pH":3.19},{"pH":3.18},{"pH":3.14},{"pH":3.06},{"pH":3.08},{"pH":3.32},{"pH":3.28},{"pH":3.22},{"pH":3.05},{"pH":3.15},{"pH":3.1},{"pH":3.16},{"pH":3.5},{"pH":2.99},{"pH":3.32},{"pH":3.24},{"pH":3.3},{"pH":3.13},{"pH":3.34},{"pH":3.05},{"pH":3.01},{"pH":3.17},{"pH":3.03},{"pH":3.15},{"pH":3.12},{"pH":3.16},{"pH":3.13},{"pH":3.2},{"pH":3.15},{"pH":3.11},{"pH":3.09},{"pH":3.13},{"pH":2.99},{"pH":3.29},{"pH":3.3},{"pH":3.28},{"pH":3.11},{"pH":2.94},{"pH":3.17},{"pH":3.41},{"pH":3.37},{"pH":3.36},{"pH":2.93},{"pH":3.05},{"pH":3.14},{"pH":3.15},{"pH":3.1},{"pH":3.06},{"pH":3.0},{"pH":3.13},{"pH":3.25},{"pH":3.26},{"pH":3.1},{"pH":3.05},{"pH":3.28},{"pH":3.33},{"pH":3.22},{"pH":3.25},{"pH":3.32},{"pH":3.14},{"pH":2.93},{"pH":3.1},{"pH":3.1},{"pH":3.18},{"pH":3.2},{"pH":3.19},{"pH":2.93},{"pH":3.28},{"pH":3.04},{"pH":3.37},{"pH":3.18},{"pH":3.27},{"pH":3.49},{"pH":3.12},{"pH":3.24},{"pH":3.11},{"pH":3.2},{"pH":2.98},{"pH":3.47},{"pH":3.0},{"pH":3.19},{"pH":3.13},{"pH":3.19},{"pH":3.09},{"pH":3.26},{"pH":3.31},{"pH":3.42},{"pH":3.33},{"pH":3.08},{"pH":3.02},{"pH":2.96},{"pH":3.14},{"pH":3.2},{"pH":3.51},{"pH":2.99},{"pH":3.14},{"pH":3.06},{"pH":3.08},{"pH":3.15},{"pH":3.11},{"pH":3.21},{"pH":3.22},{"pH":3.65},{"pH":3.25},{"pH":3.27},{"pH":3.1},{"pH":3.16},{"pH":3.23},{"pH":2.94},{"pH":3.28},{"pH":3.24},{"pH":3.07},{"pH":3.01},{"pH":2.9},{"pH":3.24},{"pH":3.52},{"pH":3.23},{"pH":3.25},{"pH":3.36},{"pH":3.5},{"pH":3.24},{"pH":3.19},{"pH":3.44},{"pH":3.24},{"pH":3.0},{"pH":3.09},{"pH":3.02},{"pH":3.39},{"pH":3.14},{"pH":3.19},{"pH":3.28},{"pH":3.17},{"pH":3.14},{"pH":3.35},{"pH":3.41},{"pH":3.04}]},"encoding":{"x":{"axis":{"title":"pH"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"lightgreen","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":"KDE plot of pH feature"},"transform":[{"counts":false,"cumulative":false,"density":"pH","maxsteps":200,"minsteps":25}],"width":350}],"title":{"anchor":"middle","offset":20,"text":"KDE plots of Features"}}

The previous analysis indicates that the alcohol feature has more extreme values than pH. Now, we will create a correlation heatmap to investigate the relationships between the features in the dataset.

correlation = Scholar.Stats.correlation_matrix(tensor_data, ddof: 1)

#Nx.Tensor<
  f64[12][12]
  EXLA.Backend<host:0, 0.3809581470.3464101900.77237>
  [
    [1.000204206657137, -0.022701925084394028, 0.28923975031725996, 0.08903887998201279, 0.02309035789846668, -0.04940594604443256, 0.09108835320911231, 0.26538519619855744, -0.42594525408939937, -0.017146485732801857, -0.12090580792461156, -0.1136860414197186],
    [-0.022701925084394028, 1.0002042066571377, -0.14950233378736394, 0.06429918773242695, 0.070525970411686, -0.0970317497617824, 0.08927873114082308, 0.027119382290178354, -0.03192188560415534, -0.035735442831260074, 0.06773177122976645, -0.19476273264768545],
    [0.28923975031725996, -0.14950233378736394, 1.000204206657138, 0.09423086293135367, 0.11438780236851878, 0.09409643220951228, 0.12115553337968561, 0.14953309999019224, -0.16378164987548596, 0.062343668678184735, -0.07574419436799362, -0.009210971441640103],
    [0.08903887998201279, 0.06429918773242695, 0.09423086293135367, 1.0002042066571373, 0.0887026459138499, 0.29915943156848096, 0.40152128773970025, 0.8391377774397895, -0.1941730973339338, -0.026669810894874028, -0.4507232439271815, -0.09759675473273582],
    [0.02309035789846668, 0.070525970411686, ...],
    ...
  ]
>

{corr_size, _} = Nx.shape(correlation)
correlation_list = Nx.to_flat_list(correlation)
column_names = DF.names(df_data)

corr_to_plot =
  DF.new(
    x: List.flatten(List.duplicate(column_names, corr_size)),
    y: List.flatten(for name <- column_names, do: List.duplicate(name, corr_size)),
    corr_val: Enum.map(correlation_list, fn x -> Float.round(x, 2) end)
  )

Tucan.heatmap(corr_to_plot, "x", "y", "corr_val", annotate: true, text_color: [{nil, 0, "white"}])
|> Tucan.Scale.set_color_scheme(:inferno)
|> Tucan.Axes.set_title(:color, "Correlation")
|> Tucan.set_size(630, 630)
|> Tucan.set_title("Correlation Matrix for California Housing", offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","__tucan__":{"multilayer":true},"data":{"values":[{"corr_val":1.0,"x":"fixed acidity","y":"fixed acidity"},{"corr_val":-0.02,"x":"volatile acidity","y":"fixed acidity"},{"corr_val":0.29,"x":"citric acid","y":"fixed acidity"},{"corr_val":0.09,"x":"residual sugar","y":"fixed acidity"},{"corr_val":0.02,"x":"chlorides","y":"fixed acidity"},{"corr_val":-0.05,"x":"free sulfur dioxide","y":"fixed acidity"},{"corr_val":0.09,"x":"total sulfur dioxide","y":"fixed acidity"},{"corr_val":0.27,"x":"density","y":"fixed acidity"},{"corr_val":-0.43,"x":"pH","y":"fixed acidity"},{"corr_val":-0.02,"x":"sulphates","y":"fixed acidity"},{"corr_val":-0.12,"x":"alcohol","y":"fixed acidity"},{"corr_val":-0.11,"x":"quality","y":"fixed acidity"},{"corr_val":-0.02,"x":"fixed acidity","y":"volatile acidity"},{"corr_val":1.0,"x":"volatile acidity","y":"volatile acidity"},{"corr_val":-0.15,"x":"citric acid","y":"volatile acidity"},{"corr_val":0.06,"x":"residual sugar","y":"volatile acidity"},{"corr_val":0.07,"x":"chlorides","y":"volatile acidity"},{"corr_val":-0.1,"x":"free sulfur dioxide","y":"volatile acidity"},{"corr_val":0.09,"x":"total sulfur dioxide","y":"volatile acidity"},{"corr_val":0.03,"x":"density","y":"volatile acidity"},{"corr_val":-0.03,"x":"pH","y":"volatile acidity"},{"corr_val":-0.04,"x":"sulphates","y":"volatile acidity"},{"corr_val":0.07,"x":"alcohol","y":"volatile acidity"},{"corr_val":-0.19,"x":"quality","y":"volatile acidity"},{"corr_val":0.29,"x":"fixed acidity","y":"citric acid"},{"corr_val":-0.15,"x":"volatile acidity","y":"citric acid"},{"corr_val":1.0,"x":"citric acid","y":"citric acid"},{"corr_val":0.09,"x":"residual sugar","y":"citric acid"},{"corr_val":0.11,"x":"chlorides","y":"citric acid"},{"corr_val":0.09,"x":"free sulfur dioxide","y":"citric acid"},{"corr_val":0.12,"x":"total sulfur dioxide","y":"citric acid"},{"corr_val":0.15,"x":"density","y":"citric acid"},{"corr_val":-0.16,"x":"pH","y":"citric acid"},{"corr_val":0.06,"x":"sulphates","y":"citric acid"},{"corr_val":-0.08,"x":"alcohol","y":"citric acid"},{"corr_val":-0.01,"x":"quality","y":"citric acid"},{"corr_val":0.09,"x":"fixed acidity","y":"residual sugar"},{"corr_val":0.06,"x":"volatile acidity","y":"residual sugar"},{"corr_val":0.09,"x":"citric acid","y":"residual sugar"},{"corr_val":1.0,"x":"residual sugar","y":"residual sugar"},{"corr_val":0.09,"x":"chlorides","y":"residual sugar"},{"corr_val":0.3,"x":"free sulfur dioxide","y":"residual sugar"},{"corr_val":0.4,"x":"total sulfur dioxide","y":"residual sugar"},{"corr_val":0.84,"x":"density","y":"residual sugar"},{"corr_val":-0.19,"x":"pH","y":"residual sugar"},{"corr_val":-0.03,"x":"sulphates","y":"residual sugar"},{"corr_val":-0.45,"x":"alcohol","y":"residual sugar"},{"corr_val":-0.1,"x":"quality","y":"residual sugar"},{"corr_val":0.02,"x":"fixed acidity","y":"chlorides"},{"corr_val":0.07,"x":"volatile acidity","y":"chlorides"},{"corr_val":0.11,"x":"citric acid","y":"chlorides"},{"corr_val":0.09,"x":"residual sugar","y":"chlorides"},{"corr_val":1.0,"x":"chlorides","y":"chlorides"},{"corr_val":0.1,"x":"free sulfur dioxide","y":"chlorides"},{"corr_val":0.2,"x":"total sulfur dioxide","y":"chlorides"},{"corr_val":0.26,"x":"density","y":"chlorides"},{"corr_val":-0.09,"x":"pH","y":"chlorides"},{"corr_val":0.02,"x":"sulphates","y":"chlorides"},{"corr_val":-0.36,"x":"alcohol","y":"chlorides"},{"corr_val":-0.21,"x":"quality","y":"chlorides"},{"corr_val":-0.05,"x":"fixed acidity","y":"free sulfur dioxide"},{"corr_val":-0.1,"x":"volatile acidity","y":"free sulfur dioxide"},{"corr_val":0.09,"x":"citric acid","y":"free sulfur dioxide"},{"corr_val":0.3,"x":"residual sugar","y":"free sulfur dioxide"},{"corr_val":0.1,"x":"chlorides","y":"free sulfur dioxide"},{"corr_val":1.0,"x":"free sulfur dioxide","y":"free sulfur dioxide"},{"corr_val":0.62,"x":"total sulfur dioxide","y":"free sulfur dioxide"},{"corr_val":0.29,"x":"density","y":"free sulfur dioxide"},{"corr_val":0.0,"x":"pH","y":"free sulfur dioxide"},{"corr_val":0.06,"x":"sulphates","y":"free sulfur dioxide"},{"corr_val":-0.25,"x":"alcohol","y":"free sulfur dioxide"},{"corr_val":0.01,"x":"quality","y":"free sulfur dioxide"},{"corr_val":0.09,"x":"fixed acidity","y":"total sulfur dioxide"},{"corr_val":0.09,"x":"volatile acidity","y":"total sulfur dioxide"},{"corr_val":0.12,"x":"citric acid","y":"total sulfur dioxide"},{"corr_val":0.4,"x":"residual sugar","y":"total sulfur dioxide"},{"corr_val":0.2,"x":"chlorides","y":"total sulfur dioxide"},{"corr_val":0.62,"x":"free sulfur dioxide","y":"total sulfur dioxide"},{"corr_val":1.0,"x":"total sulfur dioxide","y":"total sulfur dioxide"},{"corr_val":0.53,"x":"density","y":"total sulfur dioxide"},{"corr_val":0.0,"x":"pH","y":"total sulfur dioxide"},{"corr_val":0.13,"x":"sulphates","y":"total sulfur dioxide"},{"corr_val":-0.45,"x":"alcohol","y":"total sulfur dioxide"},{"corr_val":-0.17,"x":"quality","y":"total sulfur dioxide"},{"corr_val":0.27,"x":"fixed acidity","y":"density"},{"corr_val":0.03,"x":"volatile acidity","y":"density"},{"corr_val":0.15,"x":"citric acid","y":"density"},{"corr_val":0.84,"x":"residual sugar","y":"density"},{"corr_val":0.26,"x":"chlorides","y":"density"},{"corr_val":0.29,"x":"free sulfur dioxide","y":"density"},{"corr_val":0.53,"x":"total sulfur dioxide","y":"density"},{"corr_val":1.0,"x":"density","y":"density"},{"corr_val":-0.09,"x":"pH","y":"density"},{"corr_val":0.07,"x":"sulphates","y":"density"},{"corr_val":-0.78,"x":"alcohol","y":"density"},{"corr_val":-0.31,"x":"quality","y":"density"},{"corr_val":-0.43,"x":"fixed acidity","y":"pH"},{"corr_val":-0.03,"x":"volatile acidity","y":"pH"},{"corr_val":-0.16,"x":"citric acid","y":"pH"},{"corr_val":-0.19,"x":"residual sugar","y":"pH"},{"corr_val":-0.09,"x":"chlorides","y":"pH"},{"corr_val":0.0,"x":"free sulfur dioxide","y":"pH"},{"corr_val":0.0,"x":"total sulfur dioxide","y":"pH"},{"corr_val":-0.09,"x":"density","y":"pH"},{"corr_val":1.0,"x":"pH","y":"pH"},{"corr_val":0.16,"x":"sulphates","y":"pH"},{"corr_val":0.12,"x":"alcohol","y":"pH"},{"corr_val":0.1,"x":"quality","y":"pH"},{"corr_val":-0.02,"x":"fixed acidity","y":"sulphates"},{"corr_val":-0.04,"x":"volatile acidity","y":"sulphates"},{"corr_val":0.06,"x":"citric acid","y":"sulphates"},{"corr_val":-0.03,"x":"residual sugar","y":"sulphates"},{"corr_val":0.02,"x":"chlorides","y":"sulphates"},{"corr_val":0.06,"x":"free sulfur dioxide","y":"sulphates"},{"corr_val":0.13,"x":"total sulfur dioxide","y":"sulphates"},{"corr_val":0.07,"x":"density","y":"sulphates"},{"corr_val":0.16,"x":"pH","y":"sulphates"},{"corr_val":1.0,"x":"sulphates","y":"sulphates"},{"corr_val":-0.02,"x":"alcohol","y":"sulphates"},{"corr_val":0.05,"x":"quality","y":"sulphates"},{"corr_val":-0.12,"x":"fixed acidity","y":"alcohol"},{"corr_val":0.07,"x":"volatile acidity","y":"alcohol"},{"corr_val":-0.08,"x":"citric acid","y":"alcohol"},{"corr_val":-0.45,"x":"residual sugar","y":"alcohol"},{"corr_val":-0.36,"x":"chlorides","y":"alcohol"},{"corr_val":-0.25,"x":"free sulfur dioxide","y":"alcohol"},{"corr_val":-0.45,"x":"total sulfur dioxide","y":"alcohol"},{"corr_val":-0.78,"x":"density","y":"alcohol"},{"corr_val":0.12,"x":"pH","y":"alcohol"},{"corr_val":-0.02,"x":"sulphates","y":"alcohol"},{"corr_val":1.0,"x":"alcohol","y":"alcohol"},{"corr_val":0.44,"x":"quality","y":"alcohol"},{"corr_val":-0.11,"x":"fixed acidity","y":"quality"},{"corr_val":-0.19,"x":"volatile acidity","y":"quality"},{"corr_val":-0.01,"x":"citric acid","y":"quality"},{"corr_val":-0.1,"x":"residual sugar","y":"quality"},{"corr_val":-0.21,"x":"chlorides","y":"quality"},{"corr_val":0.01,"x":"free sulfur dioxide","y":"quality"},{"corr_val":-0.17,"x":"total sulfur dioxide","y":"quality"},{"corr_val":-0.31,"x":"density","y":"quality"},{"corr_val":0.1,"x":"pH","y":"quality"},{"corr_val":0.05,"x":"sulphates","y":"quality"},{"corr_val":0.44,"x":"alcohol","y":"quality"},{"corr_val":1.0,"x":"quality","y":"quality"}]},"height":630,"layer":[{"encoding":{"color":{"aggregate":"mean","axis":{"title":"Correlation"},"field":"corr_val","scale":{"reverse":false,"scheme":"inferno"},"type":"quantitative"},"x":{"field":"x","type":"nominal"},"y":{"field":"y","type":"nominal"}},"mark":{"fillOpacity":1,"type":"rect"}},{"encoding":{"color":{"aggregate":"mean","axis":{"title":"Correlation"},"condition":[{"test":"datum['mean_corr_val'] < 0","value":"white"},{"test":"true","value":"black"}],"field":"corr_val","scale":{"reverse":false,"scheme":"inferno"},"type":"quantitative"},"text":{"aggregate":"mean","field":"corr_val","type":"quantitative"},"x":{"field":"x","type":"nominal"},"y":{"field":"y","type":"nominal"}},"mark":"text"}],"title":{"offset":20,"text":"Correlation Matrix for California Housing"},"width":630}

We can observe from the correlation heatmap that there is no strong correlation between the quality of wine and any single feature. However, we can see that there are two strong correlations: density is proportional to the amount of residual sugar and inversely proportional to the amount of alcohol.

Given that citric acid, free sulfur dioxide, and sulphates are not strongly correlated with the quality of wine or any other features, we can drop them from the dataset to simplify our analysis.

Before dropping the features, it is important to consider their potential impact on the final prediction. Even if they are not strongly correlated with the target variable (quality), they may still provide useful information for the KNN algorithm. It is recommended to experiment with different feature subsets to find the optimal combination for the given task. You can try running the notebook again without dropping these features.

tensor_data =
  DF.discard(df_data, ["citric acid", "free sulfur dioxide", "sulphates"]) |> Nx.stack(axis: 1)

#Nx.Tensor<
  f64[4898][9]
  EXLA.Backend<host:0, 0.3809581470.3464101900.77289>
  [
    [7.0, 0.27, 20.7, 0.045, 170.0, 1.001, 3.0, 8.8, 6.0],
    [6.3, 0.3, 1.6, 0.049, 132.0, 0.994, 3.3, 9.5, 6.0],
    [8.1, 0.28, 6.9, 0.05, 97.0, 0.9951, 3.26, 10.1, 6.0],
    [7.2, 0.23, 8.5, 0.058, 186.0, 0.9956, 3.19, 9.9, 6.0],
    [7.2, 0.23, 8.5, 0.058, 186.0, 0.9956, 3.19, 9.9, 6.0],
    [8.1, 0.28, 6.9, 0.05, 97.0, ...],
    ...
  ]
>

The next step will be splitting the dataset into features and labels. To make the classification task easier, we will convert the labels into three categories: "poor," "medium," and "excellent". Additionally, we will normalize the features using the standard scaler.

x = tensor_data[[.., 0..-2//1]]
y = tensor_data[[.., -1]]

# convert quality into labels quality: (0, 4) poor => 0, (5, 6) medium => 1, (7, 10) excelent => 2

poor_and_better_mask = Nx.greater(y, 4)
medium_and_better_mask = Nx.greater(y, 6)

y = Nx.select(poor_and_better_mask, Nx.select(medium_and_better_mask, 2, 1), 0)
x = Scholar.Preprocessing.standard_scale(x)

{x, y}

{#Nx.Tensor<
   f64[4898][8]
   EXLA.Backend<host:0, 0.3809581470.3464101900.77349>
   [
     [-0.29385297541380284, -0.4368649169854585, -0.0027291121847267076, -0.44164614831586296, 3.1698834995014824, -0.4213312276408997, -0.37885264350988346, -0.2556031247705665],
     [-0.30872791733061694, -0.43622741947473787, -0.40860252734351166, -0.4415611486477669, 2.3623866525887167, -0.4214799770600679, -0.3724776684026774, -0.24072818285375244],
     [-0.27047806668738067, -0.43665241781521824, -0.29597796711620483, -0.4415398987307429, 1.6186395567480112, -0.42145660215134145, -0.37332766508363824, -0.22797823263934036],
     [-0.2896029920089988, -0.4377149136664193, -0.2619780998777726, -0.44136989939455074, 3.509882171885805, -0.42144597719282945, -0.3748151592753196, -0.23222821604414437],
     [-0.2896029920089988, -0.4377149136664193, -0.2619780998777726, -0.44136989939455074, 3.509882171885805, -0.42144597719282945, -0.3748151592753196, -0.23222821604414437],
     [-0.27047806668738067, -0.43665241781521824, -0.29597796711620483, -0.4415398987307429, 1.6186395567480112, -0.42145660215134145, -0.37332766508363824, -0.22797823263934036],
     [-0.310852909033019, ...],
     ...
   ]
 >,
 #Nx.Tensor<
   s64[4898]
   EXLA.Backend<host:0, 0.3809581470.3464101900.77326>
   [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, ...]
 >}

After performing EDA on our wine dataset, we can now train our KNN model and make predictions. However, the question arises as to what value of neighbors should we choose for the KNN model. To answer this question, we will use K-Fold Cross-Validation (specifically, Nested Cross-Validation). K-Fold is a procedure performed on the training dataset where we split the data into k smaller subsets (folds). For each tested parameter value, we run k separate trainings and testings, where one fold is the validation (test) dataset, and the other k-1 folds are the training dataset. To make this process clear, there is a GIF below that explains it visually.

Figure 3: Illustration of KFold Cross-Validation when n = 12 observations and k = 3. After data is shuffled, a total of 3 models will be trained and tested.

defmodule Comb do
  def combinations([]), do: [[]]

  def combinations([{name, values} | opts]) do
    for subcombination <- combinations(opts), value <- values do
      [{name, value} | subcombination]
    end
  end
end

Comb.combinations(task: [:classification], num_classes: [3], num_neighbors: Enum.to_list(1..30))

[
  [task: :classification, num_classes: 3, num_neighbors: 1],
  [task: :classification, num_classes: 3, num_neighbors: 2],
  [task: :classification, num_classes: 3, num_neighbors: 3],
  [task: :classification, num_classes: 3, num_neighbors: 4],
  [task: :classification, num_classes: 3, num_neighbors: 5],
  [task: :classification, num_classes: 3, num_neighbors: 6],
  [task: :classification, num_classes: 3, num_neighbors: 7],
  [task: :classification, num_classes: 3, num_neighbors: 8],
  [task: :classification, num_classes: 3, num_neighbors: 9],
  [task: :classification, num_classes: 3, num_neighbors: 10],
  [task: :classification, num_classes: 3, num_neighbors: 11],
  [task: :classification, num_classes: 3, num_neighbors: 12],
  [task: :classification, num_classes: 3, num_neighbors: 13],
  [task: :classification, num_classes: 3, num_neighbors: 14],
  [task: :classification, num_classes: 3, num_neighbors: 15],
  [task: :classification, num_classes: 3, num_neighbors: 16],
  [task: :classification, num_classes: 3, num_neighbors: 17],
  [task: :classification, num_classes: 3, num_neighbors: 18],
  [task: :classification, num_classes: 3, num_neighbors: 19],
  [task: :classification, num_classes: 3, num_neighbors: 20],
  [task: :classification, num_classes: 3, num_neighbors: 21],
  [task: :classification, num_classes: 3, num_neighbors: 22],
  [task: :classification, num_classes: 3, num_neighbors: 23],
  [task: :classification, num_classes: 3, num_neighbors: 24],
  [task: :classification, num_classes: 3, num_neighbors: 25],
  [task: :classification, num_classes: 3, num_neighbors: 26],
  [task: :classification, num_classes: 3, num_neighbors: 27],
  [task: :classification, num_classes: 3, num_neighbors: 28],
  [task: :classification, num_classes: 3, num_neighbors: 29],
  [task: :classification, num_classes: 3, num_neighbors: 30]
]

The code implementing KFold cross-validation is located at the beginning of the notebook.

min_num_neighbors = 1
param_space_size = 30

# K in KFold
k = 10
train_size = 4000

{indices, _new_key} = Nx.Random.shuffle(key, Nx.iota(Nx.shape(y)))
x = Nx.take(x, indices)
y = Nx.take(y, indices)
{train_data, test_data} = Nx.split(x, train_size)
{train_labels, test_labels} = Nx.split(y, train_size)

folding_fun = fn x -> Scholar.ModelSelection.k_fold_split(x, k) end

scoring_fun = fn x, y, opts ->
  {x_train, x_test} = x
  {y_train, y_test} = y

  model =
    KNNClassifier.fit(x_train, y_train,
      num_classes: opts[:num_classes],
      num_neighbors: opts[:num_neighbors],
      algorithm: :brute
    )

  prediction = KNNClassifier.predict(model, x_test)

  accuracy = Classification.accuracy(y_test, prediction)
  [accuracy]
end

res =
  Scholar.ModelSelection.grid_search(train_data, train_labels, folding_fun, scoring_fun,
    num_classes: [3],
    num_neighbors: Enum.to_list(min_num_neighbors..param_space_size)
  )

res = for(sub_res <- res, do: sub_res[:score]) |> Nx.concatenate() |> Nx.as_type(:f64)

results =
  DF.new(accuracy: res, num_neighbors: Nx.add(Nx.iota({param_space_size}), min_num_neighbors))

#Explorer.DataFrame<
  Polars[30 x 2]
  accuracy f64 [0.7682499885559082, 0.734250009059906, 0.7425000071525574, 0.7512499690055847, 0.7512499690055847, ...]
  num_neighbors s64 [1, 2, 3, 4, 5, ...]
>

To potentially improve our KNN model's performance, we can try setting the weights parameter to :distance and use weighted version of grid search. Next, we can visualize the results of KFold using a plot.

Tucan.lineplot(results, "num_neighbors", "accuracy",
  line_color: "gray",
  points: true,
  stroke_dash: [5, 5]
)
|> Tucan.Scale.set_x_domain(1, 31)
|> Tucan.Scale.set_y_domain(0.7, 0.85)
|> Tucan.set_size(630, 630)
|> Tucan.set_title("Accuracy vs Number of Neighbors", offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","data":{"values":[{"accuracy":0.7682499885559082,"num_neighbors":1},{"accuracy":0.734250009059906,"num_neighbors":2},{"accuracy":0.7425000071525574,"num_neighbors":3},{"accuracy":0.7512499690055847,"num_neighbors":4},{"accuracy":0.7512499690055847,"num_neighbors":5},{"accuracy":0.749750018119812,"num_neighbors":6},{"accuracy":0.7477499842643738,"num_neighbors":7},{"accuracy":0.7487500309944153,"num_neighbors":8},{"accuracy":0.7487500309944153,"num_neighbors":9},{"accuracy":0.749250054359436,"num_neighbors":10},{"accuracy":0.7489999532699585,"num_neighbors":11},{"accuracy":0.7477499842643738,"num_neighbors":12},{"accuracy":0.7475000023841858,"num_neighbors":13},{"accuracy":0.7419999837875366,"num_neighbors":14},{"accuracy":0.7487500309944153,"num_neighbors":15},{"accuracy":0.747249960899353,"num_neighbors":16},{"accuracy":0.7505000233650208,"num_neighbors":17},{"accuracy":0.7475000023841858,"num_neighbors":18},{"accuracy":0.7475000023841858,"num_neighbors":19},{"accuracy":0.7477499842643738,"num_neighbors":20},{"accuracy":0.7480000257492065,"num_neighbors":21},{"accuracy":0.7477499842643738,"num_neighbors":22},{"accuracy":0.7459999918937683,"num_neighbors":23},{"accuracy":0.7442499995231628,"num_neighbors":24},{"accuracy":0.7442499995231628,"num_neighbors":25},{"accuracy":0.7437499761581421,"num_neighbors":26},{"accuracy":0.7434999942779541,"num_neighbors":27},{"accuracy":0.7464999556541443,"num_neighbors":28},{"accuracy":0.7430000305175781,"num_neighbors":29},{"accuracy":0.747249960899353,"num_neighbors":30}]},"encoding":{"x":{"field":"num_neighbors","scale":{"domain":[1,31]},"type":"quantitative"},"y":{"field":"accuracy","scale":{"domain":[0.7,0.85]},"type":"quantitative"}},"height":630,"mark":{"color":"gray","fillOpacity":1,"point":[],"strokeDash":[5,5],"type":"line"},"title":{"offset":20,"text":"Accuracy vs Number of Neighbors"},"width":630}

best_neighbors = Nx.add(Nx.argmax(res), min_num_neighbors) |> Nx.to_number()

1

Ok, let's test our best model on test data.

best_model =
  KNNClassifier.fit(train_data, train_labels,
    num_neighbors: best_neighbors,
    num_classes: 3,
    algorithm: :brute
  )

final_prediction = KNNClassifier.predict(best_model, test_data)
Classification.accuracy(test_labels, final_prediction)

#Nx.Tensor<
  f32
  EXLA.Backend<host:0, 0.3809581470.3464101899.76876>
  0.7672605514526367
>

Pretty well, now let's move on to a regression task using KNN.

Regression

KNNs can also be used in regression tasks. We will explore this on a dataset about Airfoil Self-Noise. Here's a brief description of the dataset:

Data Set Information:

The NASA data set comprises different size NACA 0012 airfoils at various wind tunnel speeds and angles of attack. The span of the airfoil and the observer position were the same in all of the experiments.

Attribute Information:

This problem has the following inputs:

1. Frequency, in Hertzs.
2. Angle of attack, in degrees.
3. Chord length, in meters.
4. Free-stream velocity, in meters per second.
5. Suction side displacement thickness, in meters.

The only output is:

1. Scaled sound pressure level, in decibels.

Dua, D. and Graff, C. (2019). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.

dataset =
  Req.get!(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/00291/airfoil_self_noise.dat"
  ).body

column_names = [
  "frequency",
  "angle_of_attack",
  "chord_length",
  "free_stream_velocity",
  "suction_side_displacement_thickness",
  "scaled_sound_pressure_level"
]

dataset_df = DF.load_csv!(dataset, header: false, delimiter: "\t") |> DF.rename(column_names)
labels = DF.select(dataset_df, "scaled_sound_pressure_level")
data = DF.discard(dataset_df, "scaled_sound_pressure_level")

#Explorer.DataFrame<
  Polars[1503 x 5]
  frequency s64 [800, 1000, 1250, 1600, 2000, ...]
  angle_of_attack f64 [0.0, 0.0, 0.0, 0.0, 0.0, ...]
  chord_length f64 [0.3048, 0.3048, 0.3048, 0.3048, 0.3048, ...]
  free_stream_velocity f64 [71.3, 71.3, 71.3, 71.3, 71.3, ...]
  suction_side_displacement_thickness f64 [0.00266337, 0.00266337, 0.00266337, 0.00266337, 0.00266337, ...]
>

Below are the KDE plots of the dataset's features. We will analyze them in the next step.

Tucan.concat(
  [
    Tucan.density(data, "frequency", fill_color: "lightblue", only: ["frequency"])
    |> Tucan.Axes.set_x_title("Frequency (Hz)")
    |> Tucan.set_size(350, 300)
    |> Tucan.set_title("KDE plot of Frequency feature", offset: 20),
    Tucan.density(data, "free_stream_velocity",
      fill_color: "purple",
      only: ["free_stream_velocity"]
    )
    |> Tucan.Axes.set_x_title("Angle of attack")
    |> Tucan.set_size(350, 300)
    |> Tucan.set_title("KDE plot of Angle of Attack feature", offset: 20),
    Tucan.density(data, "angle_of_attack", fill_color: "lightgreen", only: ["angle_of_attack"])
    |> Tucan.Axes.set_x_title("Angle of attack")
    |> Tucan.set_size(350, 300)
    |> Tucan.set_title("KDE plot of Angle of Attack feature", offset: 20),
    Tucan.density(data, "suction_side_displacement_thickness",
      fill_color: "red",
      only: ["suction_side_displacement_thickness"]
    )
    |> Tucan.Axes.set_x_title("Suction Side Displacement Thickness")
    |> Tucan.set_size(350, 300)
    |> Tucan.set_title("KDE plot of Suction Side Displacement\nThickness feature", offset: 20)
  ],
  columns: 2
)
|> Tucan.set_title("KDE plots of Features", anchor: :middle, offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","columns":2,"concat":[{"data":{"values":[{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":16000},{"frequency":20000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":12500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":10000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":8000},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":200},{"frequency":250},{"frequency":315},{"frequency":400},{"frequency":500},{"frequency":630},{"frequency":800},{"frequency":1000},{"frequency":1250},{"frequency":1600},{"frequency":2000},{"frequency":2500},{"frequency":3150},{"frequency":4000},{"frequency":5000},{"frequency":6300}]},"encoding":{"x":{"axis":{"title":"Frequency (Hz)"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"lightblue","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":"KDE plot of Frequency feature"},"transform":[{"counts":false,"cumulative":false,"density":"frequency","maxsteps":200,"minsteps":25}],"width":350},{"data":{"values":[{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":55.5},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":31.7},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":71.3},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6},{"free_stream_velocity":39.6}]},"encoding":{"x":{"axis":{"title":"Angle of attack"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"purple","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":"KDE plot of Angle of Attack feature"},"transform":[{"counts":false,"cumulative":false,"density":"free_stream_velocity","maxsteps":200,"minsteps":25}],"width":350},{"data":{"values":[{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":1.5},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":3.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":2.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":4.0},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":5.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":7.3},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":2.7},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":5.4},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":7.2},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":9.9},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":12.6},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":4.2},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":8.4},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":11.2},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":15.4},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":19.7},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":4.8},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":9.5},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":12.7},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":17.4},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":22.2},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":0.0},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":3.3},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":6.7},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":8.9},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":12.3},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6},{"angle_of_attack":15.6}]},"encoding":{"x":{"axis":{"title":"Angle of attack"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"lightgreen","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":"KDE plot of Angle of Attack feature"},"transform":[{"counts":false,"cumulative":false,"density":"angle_of_attack","maxsteps":200,"minsteps":25}],"width":350},{"data":{"values":[{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00266337},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00283081},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00310138},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00331266},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00336729},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00392107},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00425727},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00452492},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00495741},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00497773},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00579636},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00214345},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00229336},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.00253511},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.0027238},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00293031},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00313525},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00346574},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00372371},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.00400603},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.0042862},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00473801},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.00509068},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.0051942},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.00614329},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0104404},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0111706},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0123481},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0132672},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.0015988},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00172668},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00193287},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00209405},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00243851},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00294804},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00401199},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00433288},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00485029},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00525474},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00752039},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.00909175},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0193001},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0208438},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0233328},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0252785},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0483159},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":0.0584113},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.40478e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.6193e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":7.91822e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":8.12164e-4},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00142788},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00152689},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00529514},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00544854},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00566229},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.00580776},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.014072},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0150478},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0264269},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0271925},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0282593},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0289853},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.0341183},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":0.036484},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.00682e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.1229e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.28464e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":4.39472e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.48633e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":8.73218e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.07475e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":9.30789e-4},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.00420654},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.0043284},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00449821},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.00461377},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0121808},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.0130253},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.016104},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0165706},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0172206},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0176631},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0214178},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.0229028},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00121072},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00131983},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00146332},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00150092},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.00202822},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.002211},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00245138},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00251435},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.00478288},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.0052139},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00578076},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.00592927},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0103088},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0124596},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0337792},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0368233},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0408268},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0418756},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0437259},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487},{"suction_side_displacement_thickness":0.0528487}]},"encoding":{"x":{"axis":{"title":"Suction Side Displacement Thickness"},"field":"value","scale":{"zero":false},"type":"quantitative"},"y":{"field":"density","stack":null,"type":"quantitative"}},"height":300,"mark":{"color":"red","fillOpacity":1,"orient":"vertical","type":"area"},"title":{"offset":20,"text":["KDE plot of Suction Side Displacement","Thickness feature"]},"transform":[{"counts":false,"cumulative":false,"density":"suction_side_displacement_thickness","maxsteps":200,"minsteps":25}],"width":350}],"title":{"anchor":"middle","offset":20,"text":"KDE plots of Features"}}

The Suction Side Displacement Thickness and Frequency features have asymmetric distributions with many observations having small values. To make these distributions less skewed, we will use the logarithms of these two features.

data =
  DF.mutate(data,
    frequency_log: log(frequency),
    suction_side_displacement_thickness_log: log(suction_side_displacement_thickness)
  )

data = DF.discard(data, ["frequency", "suction_side_displacement_thickness"])

#Explorer.DataFrame<
  Polars[1503 x 5]
  angle_of_attack f64 [0.0, 0.0, 0.0, 0.0, 0.0, ...]
  chord_length f64 [0.3048, 0.3048, 0.3048, 0.3048, 0.3048, ...]
  free_stream_velocity f64 [71.3, 71.3, 71.3, 71.3, 71.3, ...]
  frequency_log f64 [6.684611727667927, 6.907755278982137, 7.1308988302963465, 7.3777589082278725, 7.600902459542082, ...]
  suction_side_displacement_thickness_log f64 [-5.928163040757819, -5.928163040757819, -5.928163040757819, -5.928163040757819, -5.928163040757819, ...]
>

Scale data and convert them to tensors.

x = Nx.stack(data, axis: 1) |> Scholar.Preprocessing.standard_scale()
y = Nx.stack(labels, axis: 1)
{x, y}

{#Nx.Tensor<
   f64[1503][5]
   EXLA.Backend<host:0, 0.3809581470.3464101898.76836>
   [
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.24959453243691035, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.2391306895323175, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.22866684662772468, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.21709086757891163, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.2066270246743188, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.19616318176972597, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.18532568847301975, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.17412335981632007, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.1636595169117272, -0.8410438169469526],
     [-0.5630552019680845, -0.5487622533323925, 2.780406864058286, -0.15282202361502104, ...],
     ...
   ]
 >,
 #Nx.Tensor<
   f64[1503][1]
   EXLA.Backend<host:0, 0.3809581470.3464101898.76838>
   [
     [126.201],
     [125.201],
     [125.951],
     [127.591],
     [127.461],
     [125.571],
     [125.201],
     [123.061],
     [121.301],
     [119.541],
     [117.151],
     [115.391],
     [112.241],
     [108.721],
     [126.416],
     [127.696],
     [128.086],
     [126.966],
     [126.086],
     [126.986],
     [126.616],
     [124.106],
     [123.236],
     [121.106],
     [119.606],
     [117.976],
     [116.476],
     [113.076],
     [111.076],
     [118.129],
     [119.319],
     [122.779],
     [124.809],
     [126.959],
     [128.629],
     [129.099],
     [127.899],
     [125.499],
     [124.049],
     [123.689],
     [121.399],
     [120.319],
     [119.229],
     [117.789],
     [116.229],
     [114.779],
     [112.139],
     [109.619],
     ...
   ]
 >}

In this section, we will apply a similar KFold procedure as in the classification section to find the best value for the :num_neighbors parameter in the KNN regression model.

min_num_neighbors = 1
param_space_size = 30

# K in KFold
k = 10
train_size = 1100

{indices, _new_key} = Nx.Random.shuffle(key, Nx.iota({Nx.axis_size(y, 0)}))
x_shuffled = Nx.take(x, indices)
y_shuffled = Nx.take(y, indices)
{train_data, test_data} = Nx.split(x_shuffled, train_size)
{train_labels, test_labels} = Nx.split(y_shuffled, train_size)

folding_fun = fn x -> Scholar.ModelSelection.k_fold_split(x, k) end

scoring_fun = fn x, y, opts ->
  {x_train, x_test} = x
  {y_train, y_test} = y

  model =
    KNNRegressor.fit(x_train, y_train,
      num_neighbors: opts[:num_neighbors],
      algorithm: :brute
    )

  prediction = KNNRegressor.predict(model, x_test)

  rmse = Regression.mean_square_error(y_test, prediction) |> Nx.sqrt()
  [rmse]
end

res =
  Scholar.ModelSelection.grid_search(train_data, train_labels, folding_fun, scoring_fun,
    num_neighbors: Enum.to_list(min_num_neighbors..param_space_size)
  )

res = for(sub_res <- res, do: sub_res[:score]) |> Nx.concatenate() |> Nx.as_type(:f64)

results = DF.new(RMSE: res, num_neighbors: Nx.add(Nx.iota({param_space_size}), min_num_neighbors))

#Explorer.DataFrame<
  Polars[30 x 2]
  RMSE f64 [2.937686338850874, 2.7219191542128343, 3.0070456462694466, 3.2797595466547955, 3.5000406284165377, ...]
  num_neighbors s64 [1, 2, 3, 4, 5, ...]
>

Tucan.lineplot(results, "num_neighbors", "RMSE",
  points: true,
  stroke_dash: [5, 5],
  line_color: "gray"
)
|> Tucan.Scale.set_x_domain(1, 31)
|> Tucan.Scale.set_y_domain(2.6, 6.0)
|> Tucan.set_size(630, 630)
|> Tucan.set_title("RMSE vs. Number of Neighbors", offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","data":{"values":[{"RMSE":2.937686338850874,"num_neighbors":1},{"RMSE":2.7219191542128343,"num_neighbors":2},{"RMSE":3.0070456462694466,"num_neighbors":3},{"RMSE":3.2797595466547955,"num_neighbors":4},{"RMSE":3.5000406284165377,"num_neighbors":5},{"RMSE":3.6966070105636155,"num_neighbors":6},{"RMSE":3.874724084122994,"num_neighbors":7},{"RMSE":4.043290822766933,"num_neighbors":8},{"RMSE":4.1899633048271046,"num_neighbors":9},{"RMSE":4.314402882706438,"num_neighbors":10},{"RMSE":4.436232613315821,"num_neighbors":11},{"RMSE":4.56903058537768,"num_neighbors":12},{"RMSE":4.67183935041025,"num_neighbors":13},{"RMSE":4.788191604258063,"num_neighbors":14},{"RMSE":4.8795080608911245,"num_neighbors":15},{"RMSE":4.979955872841223,"num_neighbors":16},{"RMSE":5.0613932995624085,"num_neighbors":17},{"RMSE":5.160778896481933,"num_neighbors":18},{"RMSE":5.237119460732094,"num_neighbors":19},{"RMSE":5.288934229402132,"num_neighbors":20},{"RMSE":5.340232053799357,"num_neighbors":21},{"RMSE":5.396086809176907,"num_neighbors":22},{"RMSE":5.441999665594574,"num_neighbors":23},{"RMSE":5.4796131543506,"num_neighbors":24},{"RMSE":5.522608438898208,"num_neighbors":25},{"RMSE":5.567948311102837,"num_neighbors":26},{"RMSE":5.602514299061302,"num_neighbors":27},{"RMSE":5.6423885412466515,"num_neighbors":28},{"RMSE":5.674949067282498,"num_neighbors":29},{"RMSE":5.709419328767913,"num_neighbors":30}]},"encoding":{"x":{"field":"num_neighbors","scale":{"domain":[1,31]},"type":"quantitative"},"y":{"field":"RMSE","scale":{"domain":[2.6,6.0]},"type":"quantitative"}},"height":630,"mark":{"color":"gray","fillOpacity":1,"point":[],"strokeDash":[5,5],"type":"line"},"title":{"offset":20,"text":"RMSE vs. Number of Neighbors"},"width":630}

best_neighbors = Nx.add(Nx.argmin(res), min_num_neighbors) |> Nx.to_number()

2

The best value is 2. Now try this value to a final prediction.

best_model =
  KNNRegressor.fit(train_data, train_labels,
    num_neighbors: best_neighbors,
    algorithm: :brute
  )

final_prediction = KNNRegressor.predict(best_model, test_data)
Regression.mean_square_error(test_labels, final_prediction) |> Nx.sqrt()

#Nx.Tensor<
  f64
  EXLA.Backend<host:0, 0.3809581470.3464101898.76949>
  2.243907122203796
>

Outliers prediction

KNNs can be used for outlier detection. In this task, we will also use the Airfoil Self-Noise dataset. We will calculate for each sample a mean value of distances to the three closest points from dataset.

num_samples = Nx.axis_size(x, 0)

{indices, distances} =
  BruteKNN.fit(x, num_neighbors: 4, metric: {:minkowski, 2}) |> BruteKNN.predict(x)

mean_distances = Nx.mean(distances[[.., 1..-1//1]], axes: [1], keep_axes: true)

samples_mean_distances =
  Nx.concatenate([mean_distances, Nx.iota({num_samples, 1})], axis: 1)
  |> DF.new()
  |> DF.rename(["mean_distances", "index"])

#Explorer.DataFrame<
  Polars[1503 x 2]
  mean_distances f64 [0.01831276100865005, 0.011986701521595157, 0.010944162124773065, 0.01094416212477134, 0.010573450076689597, ...]
  index f64 [0.0, 1.0, 2.0, 3.0, 4.0, ...]
>

Now, plot the mean values of distances.

Tucan.lineplot(samples_mean_distances, "index", "mean_distances", line_color: "jet")
|> Tucan.hruler(0.018, line_color: "red", stroke_dash: [5, 5])
|> Tucan.Scale.set_x_domain(0, 1510)
|> Tucan.Scale.set_y_domain(0.0085, 0.0225)
|> Tucan.set_size(800, 630)
|> Tucan.set_title("Plot to check anomalies", offset: 20)

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","data":{"values":[{"index":0.0,"mean_distances":0.01831276100865005},{"index":1.0,"mean_distances":0.011986701521595157},{"index":2.0,"mean_distances":0.010944162124773065},{"index":3.0,"mean_distances":0.01094416212477134},{"index":4.0,"mean_distances":0.010573450076689597},{"index":5.0,"mean_distances":0.010698000207391608},{"index":6.0,"mean_distances":0.010944162124805675},{"index":7.0,"mean_distances":0.010819611994103662},{"index":8.0,"mean_distances":0.010698000207391834},{"index":9.0,"mean_distances":0.010944162124698183},{"index":10.0,"mean_distances":0.010819611994050805},{"index":11.0,"mean_distances":0.010573450076634733},{"index":12.0,"mean_distances":0.010944162124767627},{"index":13.0,"mean_distances":0.012467020741492136},{"index":14.0,"mean_distances":0.012053601621272558},{"index":15.0,"mean_distances":0.010846532008318104},{"index":16.0,"mean_distances":0.010721981877558623},{"index":17.0,"mean_distances":0.010475819960193686},{"index":18.0,"mean_distances":0.010846532008248958},{"index":19.0,"mean_distances":0.01084653200830535},{"index":20.0,"mean_distances":0.010475819960193589},{"index":21.0,"mean_distances":0.010600370090842038},{"index":22.0,"mean_distances":0.010846532008207075},{"index":23.0,"mean_distances":0.010721981877586821},{"index":24.0,"mean_distances":0.010600370090869454},{"index":25.0,"mean_distances":0.01084653200823616},{"index":26.0,"mean_distances":0.012339971507078246},{"index":27.0,"mean_distances":0.014197952456828034},{"index":28.0,"mean_distances":0.018550049860226393},{"index":29.0,"mean_distances":0.018447531862904248},{"index":30.0,"mean_distances":0.012040068699160732},{"index":31.0,"mean_distances":0.01071554457263918},{"index":32.0,"mean_distances":0.01059099444193619},{"index":33.0,"mean_distances":0.010469382655304954},{"index":34.0,"mean_distances":0.010715544572625522},{"index":35.0,"mean_distances":0.010590994441922045},{"index":36.0,"mean_distances":0.010344832524558038},{"index":37.0,"mean_distances":0.010715544572627361},{"index":38.0,"mean_distances":0.010715544572627361},{"index":39.0,"mean_distances":0.010344832524558038},{"index":40.0,"mean_distances":0.010469382655261516},{"index":41.0,"mean_distances":0.010715544572625522},{"index":42.0,"mean_distances":0.010590994441936693},{"index":43.0,"mean_distances":0.010469382655261516},{"index":44.0,"mean_distances":0.010715544572638735},{"index":45.0,"mean_distances":0.012251302893483383},{"index":46.0,"mean_distances":0.014197952456813887},{"index":47.0,"mean_distances":0.018976584593715092},{"index":48.0,"mean_distances":0.018411090426490088},{"index":49.0,"mean_distances":0.011981880609049764},{"index":50.0,"mean_distances":0.0106296348214135},{"index":51.0,"mean_distances":0.01050508469071051},{"index":52.0,"mean_distances":0.010383472904051796},{"index":53.0,"mean_distances":0.010629634821384812},{"index":54.0,"mean_distances":0.01050508469071051},{"index":55.0,"mean_distances":0.010258922773347437},{"index":56.0,"mean_distances":0.010629634821402612},{"index":57.0,"mean_distances":0.010629634821417641},{"index":58.0,"mean_distances":0.010258922773318259},{"index":59.0,"mean_distances":0.010383472904036278},{"index":60.0,"mean_distances":0.0106296348214135},{"index":61.0,"mean_distances":0.01050508469071051},{"index":62.0,"mean_distances":0.010383472904036767},{"index":63.0,"mean_distances":0.010629634821399841},{"index":64.0,"mean_distances":0.012194163756520042},{"index":65.0,"mean_distances":0.018643250034561177},{"index":66.0,"mean_distances":0.018662686081234798},{"index":67.0,"mean_distances":0.014322502587488023},{"index":68.0,"mean_distances":0.014322502587426948},{"index":69.0,"mean_distances":0.014322502587540122},{"index":70.0,"mean_distances":0.014076340670150983},{"index":71.0,"mean_distances":0.014076340670049392},{"index":72.0,"mean_distances":0.01444705271805581},{"index":73.0,"mean_distances":0.014322502587434277},{"index":74.0,"mean_distances":0.014322502587490038},{"index":75.0,"mean_distances":0.014447052718191099},{"index":76.0,"mean_distances":0.014197952456765006},{"index":77.0,"mean_distances":0.014197952456702157},{"index":78.0,"mean_distances":0.014322502587375796},{"index":79.0,"mean_distances":0.022039821953283065},{"index":80.0,"mean_distances":0.01909393085682569},{"index":81.0,"mean_distances":0.014322502587521444},{"index":82.0,"mean_distances":0.014322502587524677},{"index":83.0,"mean_distances":0.01444705271822492},{"index":84.0,"mean_distances":0.01419795245682066},{"index":85.0,"mean_distances":0.014197952456828034},{"index":86.0,"mean_distances":0.014322502587538763},{"index":87.0,"mean_distances":0.014322502587524615},{"index":88.0,"mean_distances":0.014076340670150239},{"index":89.0,"mean_distances":0.014076340670160128},{"index":90.0,"mean_distances":0.01444705271823187},{"index":91.0,"mean_distances":0.014322502587514246},{"index":92.0,"mean_distances":0.014322502587531023},{"index":93.0,"mean_distances":0.014447052718258744},{"index":94.0,"mean_distances":0.014197952456833874},{"index":95.0,"mean_distances":0.014197952456828034},{"index":96.0,"mean_distances":0.02117384772655893},{"index":97.0,"mean_distances":0.02142294798793},{"index":98.0,"mean_distances":0.014447052718165121},{"index":99.0,"mean_distances":0.014447052718243958},{"index":100.0,"mean_distances":0.014197952456846153},{"index":101.0,"mean_distances":0.01419795245684266},{"index":102.0,"mean_distances":0.014322502587517263},{"index":103.0,"mean_distances":0.014322502587432383},{"index":104.0,"mean_distances":0.014076340670122194},{"index":105.0,"mean_distances":0.01407634067010403},{"index":106.0,"mean_distances":0.014447052718243958},{"index":107.0,"mean_distances":0.014322502587567787},{"index":108.0,"mean_distances":0.014322502587435402},{"index":109.0,"mean_distances":0.014447052718164259},{"index":110.0,"mean_distances":0.014568664504852962},{"index":111.0,"mean_distances":0.020885064941288865},{"index":112.0,"mean_distances":0.02142294798799041},{"index":113.0,"mean_distances":0.014447052718274464},{"index":114.0,"mean_distances":0.014447052718258744},{"index":115.0,"mean_distances":0.014197952456819726},{"index":116.0,"mean_distances":0.014197952456813405},{"index":117.0,"mean_distances":0.014322502587537402},{"index":118.0,"mean_distances":0.014322502587565697},{"index":119.0,"mean_distances":0.01407634067019268},{"index":120.0,"mean_distances":0.014076340670187934},{"index":121.0,"mean_distances":0.014447052718258744},{"index":122.0,"mean_distances":0.014322502587555755},{"index":123.0,"mean_distances":0.014322502587559316},{"index":124.0,"mean_distances":0.014447052718258744},{"index":125.0,"mean_distances":0.014568664504921116},{"index":126.0,"mean_distances":0.021544559774654054},{"index":127.0,"mean_distances":0.021790721691987976},{"index":128.0,"mean_distances":0.014322502587521444},{"index":129.0,"mean_distances":0.014322502587524677},{"index":130.0,"mean_distances":0.01444705271822492},{"index":131.0,"mean_distances":0.01419795245682066},{"index":132.0,"mean_distances":0.014197952456828034},{"index":133.0,"mean_distances":0.014322502587538763},{"index":134.0,"mean_distances":0.014322502587524615},{"index":135.0,"mean_distances":0.014076340670150239},{"index":136.0,"mean_distances":0.014076340670160128},{"index":137.0,"mean_distances":0.01444705271823187},{"index":138.0,"mean_distances":0.014322502587514246},{"index":139.0,"mean_distances":0.014322502587531023},{"index":140.0,"mean_distances":0.014447052718258744},{"index":141.0,"mean_distances":0.020758772676253655},{"index":142.0,"mean_distances":0.02179072169200802},{"index":143.0,"mean_distances":0.014322502587541606},{"index":144.0,"mean_distances":0.01432250258753151},{"index":145.0,"mean_distances":0.014447052718245083},{"index":146.0,"mean_distances":0.014197952456855093},{"index":147.0,"mean_distances":0.014197952456856329},{"index":148.0,"mean_distances":0.014322502587559982},{"index":149.0,"mean_distances":0.014322502587538763},{"index":150.0,"mean_distances":0.014076340670164384},{"index":151.0,"mean_distances":0.01407634067017379},{"index":152.0,"mean_distances":0.014447052718258744},{"index":153.0,"mean_distances":0.01432250258752746},{"index":154.0,"mean_distances":0.014322502587531023},{"index":155.0,"mean_distances":0.021547498118684293},{"index":156.0,"mean_distances":0.02179366003601801},{"index":157.0,"mean_distances":0.01456866450485498},{"index":158.0,"mean_distances":0.012232838871953493},{"index":159.0,"mean_distances":0.010697965989555492},{"index":160.0,"mean_distances":0.010944127906975297},{"index":161.0,"mean_distances":0.010819577776382783},{"index":162.0,"mean_distances":0.010573415858962978},{"index":163.0,"mean_distances":0.010944127907044724},{"index":164.0,"mean_distances":0.01094412790704645},{"index":165.0,"mean_distances":0.010573415858962978},{"index":166.0,"mean_distances":0.010697965989610356},{"index":167.0,"mean_distances":0.010944127907030159},{"index":168.0,"mean_distances":0.01081957777627133},{"index":169.0,"mean_distances":0.010697965989610356},{"index":170.0,"mean_distances":0.010944127907030159},{"index":171.0,"mean_distances":0.01081957777627133},{"index":172.0,"mean_distances":0.010573415858906391},{"index":173.0,"mean_distances":0.01209624990896037},{"index":174.0,"mean_distances":0.015898756033839227},{"index":175.0,"mean_distances":0.010715585116209373},{"index":176.0,"mean_distances":0.010591034985505407},{"index":177.0,"mean_distances":0.010469423198844433},{"index":178.0,"mean_distances":0.010715585116209373},{"index":179.0,"mean_distances":0.010591034985505407},{"index":180.0,"mean_distances":0.01034487306814047},{"index":181.0,"mean_distances":0.010715585116223938},{"index":182.0,"mean_distances":0.010715585116209791},{"index":183.0,"mean_distances":0.010344873068126323},{"index":184.0,"mean_distances":0.010469423198844433},{"index":185.0,"mean_distances":0.010715585116209373},{"index":186.0,"mean_distances":0.010591034985491262},{"index":187.0,"mean_distances":0.011706233642710012},{"index":188.0,"mean_distances":0.012190903340898895},{"index":189.0,"mean_distances":0.010944162124930228},{"index":190.0,"mean_distances":0.010573450076746184},{"index":191.0,"mean_distances":0.010698000207391608},{"index":192.0,"mean_distances":0.010944162124805675},{"index":193.0,"mean_distances":0.010819611994103662},{"index":194.0,"mean_distances":0.010698000207501107},{"index":195.0,"mean_distances":0.010944162124807455},{"index":196.0,"mean_distances":0.010819611994050805},{"index":197.0,"mean_distances":0.01057345007669132},{"index":198.0,"mean_distances":0.010944162124875366},{"index":199.0,"mean_distances":0.010944162124763915},{"index":200.0,"mean_distances":0.014379489998603875},{"index":201.0,"mean_distances":0.018981600238766935},{"index":202.0,"mean_distances":0.012163236352343726},{"index":203.0,"mean_distances":0.01060037009098058},{"index":204.0,"mean_distances":0.01084653200837185},{"index":205.0,"mean_distances":0.010721981877613347},{"index":206.0,"mean_distances":0.010475819960250272},{"index":207.0,"mean_distances":0.010846532008302828},{"index":208.0,"mean_distances":0.01084653200835922},{"index":209.0,"mean_distances":0.01047581996027847},{"index":210.0,"mean_distances":0.010600370090953262},{"index":211.0,"mean_distances":0.01084653200828814},{"index":212.0,"mean_distances":0.010721981877641543},{"index":213.0,"mean_distances":0.010600370090925066},{"index":214.0,"mean_distances":0.011705872004746959},{"index":215.0,"mean_distances":0.012042670105773153},{"index":216.0,"mean_distances":0.010590994441922045},{"index":217.0,"mean_distances":0.010469382655304468},{"index":218.0,"mean_distances":0.01071554457263918},{"index":219.0,"mean_distances":0.010590994441922045},{"index":220.0,"mean_distances":0.010344832524558038},{"index":221.0,"mean_distances":0.010715544572640146},{"index":222.0,"mean_distances":0.010715544572626001},{"index":223.0,"mean_distances":0.010344832524543891},{"index":224.0,"mean_distances":0.010469382655261516},{"index":225.0,"mean_distances":0.010715544572638735},{"index":226.0,"mean_distances":0.010590994441964053},{"index":227.0,"mean_distances":0.01046938265528932},{"index":228.0,"mean_distances":0.011385171308504851},{"index":229.0,"mean_distances":0.011898572264409144},{"index":230.0,"mean_distances":0.010505084690669004},{"index":231.0,"mean_distances":0.010383472904023501},{"index":232.0,"mean_distances":0.010629634821371596},{"index":233.0,"mean_distances":0.01050508469068315},{"index":234.0,"mean_distances":0.010258922773319143},{"index":235.0,"mean_distances":0.010629634821388465},{"index":236.0,"mean_distances":0.01062963482138935},{"index":237.0,"mean_distances":0.01025892277327582},{"index":238.0,"mean_distances":0.010383472904008472},{"index":239.0,"mean_distances":0.010629634821399841},{"index":240.0,"mean_distances":0.010505084690696364},{"index":241.0,"mean_distances":0.01038347290402262},{"index":242.0,"mean_distances":0.01117445730698896},{"index":243.0,"mean_distances":0.021422947988004804},{"index":244.0,"mean_distances":0.014447052718303212},{"index":245.0,"mean_distances":0.014447052718298594},{"index":246.0,"mean_distances":0.014197952456931034},{"index":247.0,"mean_distances":0.014197952456899249},{"index":248.0,"mean_distances":0.014322502587596708},{"index":249.0,"mean_distances":0.014322502587568413},{"index":250.0,"mean_distances":0.014076340670206577},{"index":251.0,"mean_distances":0.01407634067018696},{"index":252.0,"mean_distances":0.014447052718326392},{"index":253.0,"mean_distances":0.014322502587624375},{"index":254.0,"mean_distances":0.014322502587573956},{"index":255.0,"mean_distances":0.014447052718271755},{"index":256.0,"mean_distances":0.014568664504989273},{"index":257.0,"mean_distances":0.018908847998624065},{"index":258.0,"mean_distances":0.021422947987953005},{"index":259.0,"mean_distances":0.014447052718232739},{"index":260.0,"mean_distances":0.014447052718232316},{"index":261.0,"mean_distances":0.014197952456793297},{"index":262.0,"mean_distances":0.014197952456786074},{"index":263.0,"mean_distances":0.014322502587511826},{"index":264.0,"mean_distances":0.014322502587511826},{"index":265.0,"mean_distances":0.014076340670122194},{"index":266.0,"mean_distances":0.014076340670132323},{"index":267.0,"mean_distances":0.014447052718191099},{"index":268.0,"mean_distances":0.014322502587487134},{"index":269.0,"mean_distances":0.014322502587490038},{"index":270.0,"mean_distances":0.021547498118643076},{"index":271.0,"mean_distances":0.019093930856805642},{"index":272.0,"mean_distances":0.014322502587501283},{"index":273.0,"mean_distances":0.014322502587517846},{"index":274.0,"mean_distances":0.01444705271820476},{"index":275.0,"mean_distances":0.014197952456786225},{"index":276.0,"mean_distances":0.014197952456799738},{"index":277.0,"mean_distances":0.014322502587491966},{"index":278.0,"mean_distances":0.014322502587499038},{"index":279.0,"mean_distances":0.01407634067014329},{"index":280.0,"mean_distances":0.014076340670146471},{"index":281.0,"mean_distances":0.014447052718198046},{"index":282.0,"mean_distances":0.014322502587494084},{"index":283.0,"mean_distances":0.014322502587510532},{"index":284.0,"mean_distances":0.018850707283501397},{"index":285.0,"mean_distances":0.021790721691994808},{"index":286.0,"mean_distances":0.014322502587507299},{"index":287.0,"mean_distances":0.014322502587517364},{"index":288.0,"mean_distances":0.01444705271822492},{"index":289.0,"mean_distances":0.01419795245682066},{"index":290.0,"mean_distances":0.0141979524568212},{"index":291.0,"mean_distances":0.014322502587538763},{"index":292.0,"mean_distances":0.014322502587517542},{"index":293.0,"mean_distances":0.01407634067014329},{"index":294.0,"mean_distances":0.014076340670153056},{"index":295.0,"mean_distances":0.014447052718238136},{"index":296.0,"mean_distances":0.014322502587555755},{"index":297.0,"mean_distances":0.014322502587545657},{"index":298.0,"mean_distances":0.02154749811867063},{"index":299.0,"mean_distances":0.012220800039648634},{"index":300.0,"mean_distances":0.010944127907082789},{"index":301.0,"mean_distances":0.01081957777643564},{"index":302.0,"mean_distances":0.010573415859019566},{"index":303.0,"mean_distances":0.010944127907101314},{"index":304.0,"mean_distances":0.01094412790704645},{"index":305.0,"mean_distances":0.010573415858962978},{"index":306.0,"mean_distances":0.010697965989664993},{"index":307.0,"mean_distances":0.010944127907137655},{"index":308.0,"mean_distances":0.010819577776380776},{"index":309.0,"mean_distances":0.010697965989666944},{"index":310.0,"mean_distances":0.010944127907083018},{"index":311.0,"mean_distances":0.010819577776380776},{"index":312.0,"mean_distances":0.010573415859019566},{"index":313.0,"mean_distances":0.010944127907152462},{"index":314.0,"mean_distances":0.0126221555300541},{"index":315.0,"mean_distances":0.019014701251680543},{"index":316.0,"mean_distances":0.021422947987976514},{"index":317.0,"mean_distances":0.014447052718247146},{"index":318.0,"mean_distances":0.014447052718217527},{"index":319.0,"mean_distances":0.014197952456819726},{"index":320.0,"mean_distances":0.014197952456813405},{"index":321.0,"mean_distances":0.014322502587537402},{"index":322.0,"mean_distances":0.014322502587579842},{"index":323.0,"mean_distances":0.014076340670150489},{"index":324.0,"mean_distances":0.014076340670146471},{"index":325.0,"mean_distances":0.014447052718217527},{"index":326.0,"mean_distances":0.01432250258752746},{"index":327.0,"mean_distances":0.014322502587531023},{"index":328.0,"mean_distances":0.014447052718232316},{"index":329.0,"mean_distances":0.02191527182268331},{"index":330.0,"mean_distances":0.012042738301152434},{"index":331.0,"mean_distances":0.010591034985532771},{"index":332.0,"mean_distances":0.0104694231988859},{"index":333.0,"mean_distances":0.010715585116249907},{"index":334.0,"mean_distances":0.010591034985532771},{"index":335.0,"mean_distances":0.010344873068168763},{"index":336.0,"mean_distances":0.010715585116250875},{"index":337.0,"mean_distances":0.010715585116236727},{"index":338.0,"mean_distances":0.010344873068154617},{"index":339.0,"mean_distances":0.010469423198872238},{"index":340.0,"mean_distances":0.010715585116249461},{"index":341.0,"mean_distances":0.010591034985560131},{"index":342.0,"mean_distances":0.01046942319891469},{"index":343.0,"mean_distances":0.012286258268316497},{"index":344.0,"mean_distances":0.019162959782036148},{"index":345.0,"mean_distances":0.021793660036035997},{"index":346.0,"mean_distances":0.014568664504895518},{"index":347.0,"mean_distances":0.014322502587507299},{"index":348.0,"mean_distances":0.014322502587517364},{"index":349.0,"mean_distances":0.01444705271822492},{"index":350.0,"mean_distances":0.01419795245682066},{"index":351.0,"mean_distances":0.0141979524568212},{"index":352.0,"mean_distances":0.014322502587538763},{"index":353.0,"mean_distances":0.014322502587535224},{"index":354.0,"mean_distances":0.014076340670157436},{"index":355.0,"mean_distances":0.01407634067015659},{"index":356.0,"mean_distances":0.01444705271822492},{"index":357.0,"mean_distances":0.014322502587521444},{"index":358.0,"mean_distances":0.01432250258753151},{"index":359.0,"mean_distances":0.021547498118663685},{"index":360.0,"mean_distances":0.013663015922653047},{"index":361.0,"mean_distances":0.011590156593184598},{"index":362.0,"mean_distances":0.011836318510545807},{"index":363.0,"mean_distances":0.01171176837989843},{"index":364.0,"mean_distances":0.01146560646253722},{"index":365.0,"mean_distances":0.011836318510615255},{"index":366.0,"mean_distances":0.011836318510659215},{"index":367.0,"mean_distances":0.011465606462480635},{"index":368.0,"mean_distances":0.011590156593128011},{"index":369.0,"mean_distances":0.011836318510545807},{"index":370.0,"mean_distances":0.011711768379841845},{"index":371.0,"mean_distances":0.01159015659322661},{"index":372.0,"mean_distances":0.011836318510547587},{"index":373.0,"mean_distances":0.0130616702514738},{"index":374.0,"mean_distances":0.019213863746452464},{"index":375.0,"mean_distances":0.016486967124940514},{"index":376.0,"mean_distances":0.011530758204684887},{"index":377.0,"mean_distances":0.011406208073980925},{"index":378.0,"mean_distances":0.011284596287345844},{"index":379.0,"mean_distances":0.011530758204712206},{"index":380.0,"mean_distances":0.01140620807399507},{"index":381.0,"mean_distances":0.011160046156631062},{"index":382.0,"mean_distances":0.011530758204700385},{"index":383.0,"mean_distances":0.011530758204698031},{"index":384.0,"mean_distances":0.01116004615660277},{"index":385.0,"mean_distances":0.011284596287320392},{"index":386.0,"mean_distances":0.011530758204711762},{"index":387.0,"mean_distances":0.011406208074034224},{"index":388.0,"mean_distances":0.011284596287374138},{"index":389.0,"mean_distances":0.013324510694051295},{"index":390.0,"mean_distances":0.019564713415972126},{"index":391.0,"mean_distances":0.013673735504876779},{"index":392.0,"mean_distances":0.012838237557568714},{"index":393.0,"mean_distances":0.012713687426885396},{"index":394.0,"mean_distances":0.012592075640314997},{"index":395.0,"mean_distances":0.012838237557676208},{"index":396.0,"mean_distances":0.012713687427010135},{"index":397.0,"mean_distances":0.012467525509612984},{"index":398.0,"mean_distances":0.012838237557675805},{"index":399.0,"mean_distances":0.012838237557639867},{"index":400.0,"mean_distances":0.012467525509556395},{"index":401.0,"mean_distances":0.01259207564025841},{"index":402.0,"mean_distances":0.012838237557712148},{"index":403.0,"mean_distances":0.012713687426974193},{"index":404.0,"mean_distances":0.012592075640260362},{"index":405.0,"mean_distances":0.015677418109805896},{"index":406.0,"mean_distances":0.02142294798799041},{"index":407.0,"mean_distances":0.014447052718274464},{"index":408.0,"mean_distances":0.014447052718258744},{"index":409.0,"mean_distances":0.014322502587555755},{"index":410.0,"mean_distances":0.014322502587559316},{"index":411.0,"mean_distances":0.014447052718258744},{"index":412.0,"mean_distances":0.014197952456819726},{"index":413.0,"mean_distances":0.014197952456813405},{"index":414.0,"mean_distances":0.014322502587537402},{"index":415.0,"mean_distances":0.014322502587579842},{"index":416.0,"mean_distances":0.01407634067019268},{"index":417.0,"mean_distances":0.014076340670202081},{"index":418.0,"mean_distances":0.014447052718258744},{"index":419.0,"mean_distances":0.014322502587555755},{"index":420.0,"mean_distances":0.014322502587559316},{"index":421.0,"mean_distances":0.021547498118684293},{"index":422.0,"mean_distances":0.01682743685228078},{"index":423.0,"mean_distances":0.01227344153872676},{"index":424.0,"mean_distances":0.012519603456099372},{"index":425.0,"mean_distances":0.012395053325396872},{"index":426.0,"mean_distances":0.012273441538750448},{"index":427.0,"mean_distances":0.012519603456099372},{"index":428.0,"mean_distances":0.012395053325382726},{"index":429.0,"mean_distances":0.01214889140801965},{"index":430.0,"mean_distances":0.012519603456087615},{"index":431.0,"mean_distances":0.012519603456078075},{"index":432.0,"mean_distances":0.012148891408033798},{"index":433.0,"mean_distances":0.012273441538736787},{"index":434.0,"mean_distances":0.012519603456085715},{"index":435.0,"mean_distances":0.012395053325382726},{"index":436.0,"mean_distances":0.0122734415387363},{"index":437.0,"mean_distances":0.015095012835814325},{"index":438.0,"mean_distances":0.02142294798796728},{"index":439.0,"mean_distances":0.014447052718247129},{"index":440.0,"mean_distances":0.014447052718231752},{"index":441.0,"mean_distances":0.014322502587524918},{"index":442.0,"mean_distances":0.014322502587528091},{"index":443.0,"mean_distances":0.014447052718228395},{"index":444.0,"mean_distances":0.01419795245682066},{"index":445.0,"mean_distances":0.0141979524568212},{"index":446.0,"mean_distances":0.014322502587532369},{"index":447.0,"mean_distances":0.01432250258752883},{"index":448.0,"mean_distances":0.014076340670157436},{"index":449.0,"mean_distances":0.01407634067015659},{"index":450.0,"mean_distances":0.01444705271822492},{"index":451.0,"mean_distances":0.014322502587521444},{"index":452.0,"mean_distances":0.01432250258753151},{"index":453.0,"mean_distances":0.021547498118663685},{"index":454.0,"mean_distances":0.013534752154752827},{"index":455.0,"mean_distances":0.01139384239823551},{"index":456.0,"mean_distances":0.011764554446223152},{"index":457.0,"mean_distances":0.01176455444621124},{"index":458.0,"mean_distances":0.011393842398134247},{"index":459.0,"mean_distances":0.011518392528838212},{"index":460.0,"mean_distances":0.011764554446256008},{"index":461.0,"mean_distances":0.01164000431559672},{"index":462.0,"mean_distances":0.011518392528828253},{"index":463.0,"mean_distances":0.011764554446148516},{"index":464.0,"mean_distances":0.011640004315499186},{"index":465.0,"mean_distances":0.011393842398190834},{"index":466.0,"mean_distances":0.011764554446274304},{"index":467.0,"mean_distances":0.014459140158095254},{"index":468.0,"mean_distances":0.013802433914531271},{"index":469.0,"mean_distances":0.011621010452885},{"index":470.0,"mean_distances":0.011496460322186238},{"index":471.0,"mean_distances":0.011250298404846253},{"index":472.0,"mean_distances":0.011621010452903915},{"index":473.0,"mean_distances":0.011621010452898711},{"index":474.0,"mean_distances":0.011250298404789666},{"index":475.0,"mean_distances":0.01137484853549363},{"index":476.0,"mean_distances":0.01162101045286191},{"index":477.0,"mean_distances":0.011496460322181034},{"index":478.0,"mean_distances":0.011374848535497861},{"index":479.0,"mean_distances":0.011621010452862799},{"index":480.0,"mean_distances":0.011496460322154607},{"index":481.0,"mean_distances":0.011250298404789666},{"index":482.0,"mean_distances":0.011621010452824473},{"index":483.0,"mean_distances":0.01696371963225568},{"index":484.0,"mean_distances":0.013633944619252672},{"index":485.0,"mean_distances":0.011750343605889649},{"index":486.0,"mean_distances":0.011625793475186172},{"index":487.0,"mean_distances":0.011379631557822165},{"index":488.0,"mean_distances":0.011750343605904276},{"index":489.0,"mean_distances":0.011750343605890128},{"index":490.0,"mean_distances":0.011379631557808018},{"index":491.0,"mean_distances":0.011504181688525641},{"index":492.0,"mean_distances":0.011750343605889649},{"index":493.0,"mean_distances":0.01162579347518323},{"index":494.0,"mean_distances":0.011504181688525156},{"index":495.0,"mean_distances":0.011750343605916522},{"index":496.0,"mean_distances":0.011644002156502825},{"index":497.0,"mean_distances":0.013541888344310646},{"index":498.0,"mean_distances":0.013411849904063322},{"index":499.0,"mean_distances":0.011625539355627997},{"index":500.0,"mean_distances":0.011500989224950199},{"index":501.0,"mean_distances":0.011254827307572976},{"index":502.0,"mean_distances":0.01162553935564094},{"index":503.0,"mean_distances":0.011625539355655088},{"index":504.0,"mean_distances":0.011254827307575592},{"index":505.0,"mean_distances":0.011379377438278581},{"index":506.0,"mean_distances":0.011625539355653186},{"index":507.0,"mean_distances":0.011500989224950199},{"index":508.0,"mean_distances":0.011379377438276453},{"index":509.0,"mean_distances":0.011625539355639529},{"index":510.0,"mean_distances":0.014678931534579791},{"index":511.0,"mean_distances":0.021131226858726062},{"index":512.0,"mean_distances":0.014197952456846153},{"index":513.0,"mean_distances":0.01419795245684266},{"index":514.0,"mean_distances":0.014322502587517263},{"index":515.0,"mean_distances":0.014322502587432383},{"index":516.0,"mean_distances":0.014076340670122194},{"index":517.0,"mean_distances":0.01407634067010403},{"index":518.0,"mean_distances":0.014447052718243958},{"index":519.0,"mean_distances":0.014322502587567787},{"index":520.0,"mean_distances":0.014322502587435402},{"index":521.0,"mean_distances":0.014447052718164259},{"index":522.0,"mean_distances":0.014197952456793297},{"index":523.0,"mean_distances":0.01419795245684266},{"index":524.0,"mean_distances":0.014322502587568413},{"index":525.0,"mean_distances":0.022039821953424382},{"index":526.0,"mean_distances":0.020637160889607004},{"index":527.0,"mean_distances":0.014568664504929224},{"index":528.0,"mean_distances":0.014197952456855093},{"index":529.0,"mean_distances":0.01419795245686316},{"index":530.0,"mean_distances":0.014322502587572769},{"index":531.0,"mean_distances":0.014322502587558622},{"index":532.0,"mean_distances":0.014076340670185483},{"index":533.0,"mean_distances":0.014076340670195009},{"index":534.0,"mean_distances":0.014447052718265692},{"index":535.0,"mean_distances":0.014322502587548558},{"index":536.0,"mean_distances":0.014322502587565664},{"index":537.0,"mean_distances":0.014447052718292566},{"index":538.0,"mean_distances":0.014197952456868307},{"index":539.0,"mean_distances":0.01419795245686316},{"index":540.0,"mean_distances":0.02090749957712723},{"index":541.0,"mean_distances":0.013663015922653047},{"index":542.0,"mean_distances":0.011590156593184598},{"index":543.0,"mean_distances":0.011836318510545807},{"index":544.0,"mean_distances":0.011711768379841845},{"index":545.0,"mean_distances":0.011465606462480635},{"index":546.0,"mean_distances":0.011836318510512952},{"index":547.0,"mean_distances":0.011836318510500326},{"index":548.0,"mean_distances":0.011465606462424047},{"index":549.0,"mean_distances":0.011590156593128011},{"index":550.0,"mean_distances":0.011836318510545807},{"index":551.0,"mean_distances":0.011711768379841845},{"index":552.0,"mean_distances":0.011590156593117337},{"index":553.0,"mean_distances":0.013864816588472342},{"index":554.0,"mean_distances":0.02142294798799041},{"index":555.0,"mean_distances":0.014447052718274464},{"index":556.0,"mean_distances":0.014447052718285175},{"index":557.0,"mean_distances":0.014197952456916888},{"index":558.0,"mean_distances":0.01419795245692658},{"index":559.0,"mean_distances":0.014322502587633713},{"index":560.0,"mean_distances":0.014322502587605418},{"index":561.0,"mean_distances":0.01407634067019268},{"index":562.0,"mean_distances":0.014076340670202081},{"index":563.0,"mean_distances":0.014447052718285175},{"index":564.0,"mean_distances":0.014322502587596084},{"index":565.0,"mean_distances":0.014322502587600297},{"index":566.0,"mean_distances":0.014447052718299961},{"index":567.0,"mean_distances":0.02191527182274571},{"index":568.0,"mean_distances":0.013446122480729232},{"index":569.0,"mean_distances":0.01140620807402243},{"index":570.0,"mean_distances":0.011284596287374138},{"index":571.0,"mean_distances":0.01153075820472542},{"index":572.0,"mean_distances":0.01140620807402243},{"index":573.0,"mean_distances":0.011160046156659357},{"index":574.0,"mean_distances":0.011530758204740107},{"index":575.0,"mean_distances":0.011530758204737751},{"index":576.0,"mean_distances":0.01116004615664521},{"index":577.0,"mean_distances":0.011284596287362345},{"index":578.0,"mean_distances":0.01153075820472542},{"index":579.0,"mean_distances":0.011406208074020076},{"index":580.0,"mean_distances":0.011284596287373652},{"index":581.0,"mean_distances":0.013324510694073881},{"index":582.0,"mean_distances":0.021790721691991394},{"index":583.0,"mean_distances":0.014322502587524918},{"index":584.0,"mean_distances":0.014322502587528091},{"index":585.0,"mean_distances":0.014447052718228395},{"index":586.0,"mean_distances":0.01419795245682066},{"index":587.0,"mean_distances":0.0141979524568212},{"index":588.0,"mean_distances":0.014322502587532369},{"index":589.0,"mean_distances":0.01432250258752883},{"index":590.0,"mean_distances":0.014076340670167985},{"index":591.0,"mean_distances":0.014076340670163667},{"index":592.0,"mean_distances":0.014447052718235003},{"index":593.0,"mean_distances":0.0143225025875386},{"index":594.0,"mean_distances":0.014322502587538583},{"index":595.0,"mean_distances":0.021547498118667158},{"index":596.0,"mean_distances":0.015799029896430925},{"index":597.0,"mean_distances":0.012713687426885396},{"index":598.0,"mean_distances":0.012592075640314997},{"index":599.0,"mean_distances":0.012838237557623351},{"index":600.0,"mean_distances":0.012713687426957276},{"index":601.0,"mean_distances":0.012467525509556395},{"index":602.0,"mean_distances":0.012838237557619219},{"index":603.0,"mean_distances":0.012838237557639867},{"index":604.0,"mean_distances":0.012467525509556395},{"index":605.0,"mean_distances":0.012592075640203773},{"index":606.0,"mean_distances":0.012838237557604654},{"index":607.0,"mean_distances":0.012713687426864748},{"index":608.0,"mean_distances":0.012592075640203773},{"index":609.0,"mean_distances":0.012838237557604654},{"index":610.0,"mean_distances":0.013862958996290331},{"index":611.0,"mean_distances":0.01978282757486924},{"index":612.0,"mean_distances":0.01502453772079425},{"index":613.0,"mean_distances":0.012519603456085715},{"index":614.0,"mean_distances":0.012395053325382726},{"index":615.0,"mean_distances":0.01227344153872264},{"index":616.0,"mean_distances":0.012519603456085715},{"index":617.0,"mean_distances":0.012395053325382726},{"index":618.0,"mean_distances":0.01214889140801965},{"index":619.0,"mean_distances":0.012519603456100403},{"index":620.0,"mean_distances":0.012519603456076715},{"index":621.0,"mean_distances":0.012148891408005505},{"index":622.0,"mean_distances":0.01227344153872264},{"index":623.0,"mean_distances":0.012519603456085715},{"index":624.0,"mean_distances":0.012395053325368577},{"index":625.0,"mean_distances":0.012273441538722151},{"index":626.0,"mean_distances":0.012519603456112588},{"index":627.0,"mean_distances":0.013601983769353579},{"index":628.0,"mean_distances":0.019593585128382874},{"index":629.0,"mean_distances":0.02142294798791178},{"index":630.0,"mean_distances":0.014447052718191987},{"index":631.0,"mean_distances":0.014447052718191099},{"index":632.0,"mean_distances":0.014322502587543721},{"index":633.0,"mean_distances":0.014322502587628592},{"index":634.0,"mean_distances":0.014447052718245736},{"index":635.0,"mean_distances":0.014197952456849884},{"index":636.0,"mean_distances":0.01419795245684266},{"index":637.0,"mean_distances":0.014322502587511826},{"index":638.0,"mean_distances":0.014322502587568413},{"index":639.0,"mean_distances":0.01407634067017878},{"index":640.0,"mean_distances":0.014076340670132323},{"index":641.0,"mean_distances":0.014447052718191099},{"index":642.0,"mean_distances":0.014322502587487134},{"index":643.0,"mean_distances":0.014322502587517369},{"index":644.0,"mean_distances":0.021547498118633962},{"index":645.0,"mean_distances":0.021422947987939107},{"index":646.0,"mean_distances":0.014447052718191987},{"index":647.0,"mean_distances":0.014447052718191099},{"index":648.0,"mean_distances":0.014322502587487134},{"index":649.0,"mean_distances":0.014322502587490038},{"index":650.0,"mean_distances":0.014447052718191099},{"index":651.0,"mean_distances":0.014197952456793297},{"index":652.0,"mean_distances":0.014197952456799738},{"index":653.0,"mean_distances":0.014322502587511826},{"index":654.0,"mean_distances":0.014322502587511826},{"index":655.0,"mean_distances":0.014076340670093902},{"index":656.0,"mean_distances":0.01407634067010403},{"index":657.0,"mean_distances":0.014447052718191099},{"index":658.0,"mean_distances":0.014322502587487134},{"index":659.0,"mean_distances":0.014322502587531023},{"index":660.0,"mean_distances":0.021547498118661284},{"index":661.0,"mean_distances":0.021422947987992807},{"index":662.0,"mean_distances":0.014447052718281408},{"index":663.0,"mean_distances":0.014447052718279353},{"index":664.0,"mean_distances":0.014322502587555755},{"index":665.0,"mean_distances":0.014322502587559316},{"index":666.0,"mean_distances":0.014447052718258744},{"index":667.0,"mean_distances":0.01419795245684802},{"index":668.0,"mean_distances":0.014197952456842182},{"index":669.0,"mean_distances":0.014322502587538763},{"index":670.0,"mean_distances":0.014322502587567057},{"index":671.0,"mean_distances":0.01407634067019963},{"index":672.0,"mean_distances":0.014076340670202081},{"index":673.0,"mean_distances":0.014447052718265692},{"index":674.0,"mean_distances":0.014322502587562702},{"index":675.0,"mean_distances":0.014322502587559316},{"index":676.0,"mean_distances":0.02154749811869124},{"index":677.0,"mean_distances":0.02142294798796728},{"index":678.0,"mean_distances":0.014447052718247129},{"index":679.0,"mean_distances":0.014447052718231752},{"index":680.0,"mean_distances":0.014322502587524918},{"index":681.0,"mean_distances":0.014322502587528091},{"index":682.0,"mean_distances":0.014447052718228395},{"index":683.0,"mean_distances":0.01419795245682066},{"index":684.0,"mean_distances":0.0141979524568212},{"index":685.0,"mean_distances":0.014322502587532369},{"index":686.0,"mean_distances":0.01432250258752883},{"index":687.0,"mean_distances":0.014076340670167985},{"index":688.0,"mean_distances":0.014076340670163667},{"index":689.0,"mean_distances":0.014447052718235003},{"index":690.0,"mean_distances":0.0143225025875386},{"index":691.0,"mean_distances":0.014322502587538583},{"index":692.0,"mean_distances":0.021547498118667158},{"index":693.0,"mean_distances":0.017931353015655568},{"index":694.0,"mean_distances":0.014443405380787385},{"index":695.0,"mean_distances":0.014447052718191099},{"index":696.0,"mean_distances":0.014322502587543721},{"index":697.0,"mean_distances":0.014322502587628592},{"index":698.0,"mean_distances":0.014447052718245736},{"index":699.0,"mean_distances":0.014197952456849884},{"index":700.0,"mean_distances":0.01419795245684266},{"index":701.0,"mean_distances":0.014322502587511826},{"index":702.0,"mean_distances":0.014322502587568413},{"index":703.0,"mean_distances":0.01407634067017878},{"index":704.0,"mean_distances":0.014076340670132323},{"index":705.0,"mean_distances":0.014447052718191099},{"index":706.0,"mean_distances":0.014322502587487134},{"index":707.0,"mean_distances":0.014322502587517369},{"index":708.0,"mean_distances":0.01805590314635953},{"index":709.0,"mean_distances":0.017934392268561927},{"index":710.0,"mean_distances":0.014446444633707164},{"index":711.0,"mean_distances":0.01444705271824553},{"index":712.0,"mean_distances":0.014322502587521444},{"index":713.0,"mean_distances":0.014322502587524677},{"index":714.0,"mean_distances":0.01444705271822492},{"index":715.0,"mean_distances":0.014197952456813587},{"index":716.0,"mean_distances":0.014197952456807056},{"index":717.0,"mean_distances":0.014322502587504754},{"index":718.0,"mean_distances":0.014322502587533049},{"index":719.0,"mean_distances":0.014076340670164384},{"index":720.0,"mean_distances":0.014076340670167201},{"index":721.0,"mean_distances":0.01444705271823187},{"index":722.0,"mean_distances":0.014322502587528393},{"index":723.0,"mean_distances":0.014322502587524677},{"index":724.0,"mean_distances":0.018058942399265403},{"index":725.0,"mean_distances":0.018190099963127825},{"index":726.0,"mean_distances":0.0143225025876012},{"index":727.0,"mean_distances":0.014322502587596708},{"index":728.0,"mean_distances":0.014322502587568413},{"index":729.0,"mean_distances":0.014076340670206577},{"index":730.0,"mean_distances":0.01407634067018696},{"index":731.0,"mean_distances":0.014447052718326392},{"index":732.0,"mean_distances":0.014322502587624375},{"index":733.0,"mean_distances":0.014322502587573956},{"index":734.0,"mean_distances":0.014447052718271755},{"index":735.0,"mean_distances":0.014197952456902743},{"index":736.0,"mean_distances":0.01419795245692658},{"index":737.0,"mean_distances":0.018190099963099532},{"index":738.0,"mean_distances":0.0190881792930068},{"index":739.0,"mean_distances":0.014322502587488023},{"index":740.0,"mean_distances":0.014322502587497682},{"index":741.0,"mean_distances":0.014322502587511826},{"index":742.0,"mean_distances":0.014076340670093902},{"index":743.0,"mean_distances":0.01407634067007671},{"index":744.0,"mean_distances":0.01444705271816378},{"index":745.0,"mean_distances":0.014322502587487134},{"index":746.0,"mean_distances":0.014322502587490038},{"index":747.0,"mean_distances":0.01444705271816467},{"index":748.0,"mean_distances":0.014197952456752724},{"index":749.0,"mean_distances":0.014197952456828034},{"index":750.0,"mean_distances":0.019088179293035096},{"index":751.0,"mean_distances":0.02009601433518523},{"index":752.0,"mean_distances":0.014322502587536465},{"index":753.0,"mean_distances":0.014322502587525975},{"index":754.0,"mean_distances":0.014322502587533049},{"index":755.0,"mean_distances":0.014076340670178532},{"index":756.0,"mean_distances":0.014076340670181348},{"index":757.0,"mean_distances":0.01444705271823187},{"index":758.0,"mean_distances":0.014322502587528393},{"index":759.0,"mean_distances":0.014322502587524677},{"index":760.0,"mean_distances":0.014447052718245083},{"index":761.0,"mean_distances":0.014197952456840947},{"index":762.0,"mean_distances":0.014197952456834867},{"index":763.0,"mean_distances":0.02007148884932931},{"index":764.0,"mean_distances":0.020096088415784846},{"index":765.0,"mean_distances":0.014322502587529748},{"index":766.0,"mean_distances":0.014322502587525975},{"index":767.0,"mean_distances":0.014322502587504754},{"index":768.0,"mean_distances":0.014076340670129145},{"index":769.0,"mean_distances":0.01407634067013891},{"index":770.0,"mean_distances":0.01444705271822492},{"index":771.0,"mean_distances":0.014322502587521444},{"index":772.0,"mean_distances":0.01432250258753151},{"index":773.0,"mean_distances":0.01444705271822492},{"index":774.0,"mean_distances":0.014197952456813587},{"index":775.0,"mean_distances":0.0141979524568212},{"index":776.0,"mean_distances":0.020071463631602202},{"index":777.0,"mean_distances":0.02105223593993195},{"index":778.0,"mean_distances":0.014076340670206577},{"index":779.0,"mean_distances":0.01407634067018696},{"index":780.0,"mean_distances":0.014447052718326392},{"index":781.0,"mean_distances":0.014322502587624375},{"index":782.0,"mean_distances":0.014322502587573956},{"index":783.0,"mean_distances":0.014447052718271755},{"index":784.0,"mean_distances":0.014197952456902743},{"index":785.0,"mean_distances":0.01419795245692658},{"index":786.0,"mean_distances":0.02117384772661519},{"index":787.0,"mean_distances":0.021669109905318368},{"index":788.0,"mean_distances":0.014693214635584926},{"index":789.0,"mean_distances":0.014322502587511826},{"index":790.0,"mean_distances":0.014076340670164387},{"index":791.0,"mean_distances":0.014076340670160616},{"index":792.0,"mean_distances":0.014447052718204997},{"index":793.0,"mean_distances":0.014322502587501033},{"index":794.0,"mean_distances":0.014322502587490038},{"index":795.0,"mean_distances":0.014447052718231426},{"index":796.0,"mean_distances":0.014568664504892824},{"index":797.0,"mean_distances":0.021544559774612098},{"index":798.0,"mean_distances":0.021298397857339262},{"index":799.0,"mean_distances":0.0143225025876012},{"index":800.0,"mean_distances":0.01432250258764786},{"index":801.0,"mean_distances":0.014322502587619565},{"index":802.0,"mean_distances":0.01407634067017878},{"index":803.0,"mean_distances":0.014076340670132323},{"index":804.0,"mean_distances":0.014447052718243958},{"index":805.0,"mean_distances":0.014568664504932683},{"index":806.0,"mean_distances":0.021544559774666756},{"index":807.0,"mean_distances":0.0214229479879952},{"index":808.0,"mean_distances":0.014447052718288349},{"index":809.0,"mean_distances":0.014447052718299961},{"index":810.0,"mean_distances":0.01419795245684802},{"index":811.0,"mean_distances":0.014197952456856329},{"index":812.0,"mean_distances":0.014322502587565697},{"index":813.0,"mean_distances":0.014322502587579842},{"index":814.0,"mean_distances":0.014076340670164387},{"index":815.0,"mean_distances":0.014076340670146471},{"index":816.0,"mean_distances":0.014447052718231426},{"index":817.0,"mean_distances":0.01456866450493455},{"index":818.0,"mean_distances":0.021544559774654054},{"index":819.0,"mean_distances":0.021422947987960208},{"index":820.0,"mean_distances":0.014447052718246886},{"index":821.0,"mean_distances":0.014447052718238582},{"index":822.0,"mean_distances":0.01419795245682066},{"index":823.0,"mean_distances":0.014197952456828034},{"index":824.0,"mean_distances":0.014322502587538763},{"index":825.0,"mean_distances":0.014322502587524615},{"index":826.0,"mean_distances":0.014076340670150239},{"index":827.0,"mean_distances":0.014076340670160128},{"index":828.0,"mean_distances":0.01444705271823187},{"index":829.0,"mean_distances":0.021915271822696522},{"index":830.0,"mean_distances":0.021422947987967154},{"index":831.0,"mean_distances":0.014447052718240054},{"index":832.0,"mean_distances":0.014447052718251913},{"index":833.0,"mean_distances":0.014197952456855093},{"index":834.0,"mean_distances":0.014197952456856329},{"index":835.0,"mean_distances":0.014322502587553588},{"index":836.0,"mean_distances":0.014322502587550051},{"index":837.0,"mean_distances":0.014076340670178532},{"index":838.0,"mean_distances":0.014076340670177323},{"index":839.0,"mean_distances":0.014447052718258744},{"index":840.0,"mean_distances":0.021915271822712013},{"index":841.0,"mean_distances":0.021422947988032598},{"index":842.0,"mean_distances":0.01444705271827544},{"index":843.0,"mean_distances":0.014447052718218896},{"index":844.0,"mean_distances":0.014322502587543721},{"index":845.0,"mean_distances":0.014322502587628592},{"index":846.0,"mean_distances":0.014447052718298594},{"index":847.0,"mean_distances":0.014197952456931034},{"index":848.0,"mean_distances":0.014197952456899249},{"index":849.0,"mean_distances":0.014322502587596708},{"index":850.0,"mean_distances":0.014322502587568413},{"index":851.0,"mean_distances":0.014076340670206577},{"index":852.0,"mean_distances":0.01407634067018696},{"index":853.0,"mean_distances":0.014447052718326392},{"index":854.0,"mean_distances":0.021915271822713623},{"index":855.0,"mean_distances":0.021422947987974353},{"index":856.0,"mean_distances":0.014447052718233712},{"index":857.0,"mean_distances":0.014447052718211261},{"index":858.0,"mean_distances":0.014322502587507299},{"index":859.0,"mean_distances":0.014322502587531023},{"index":860.0,"mean_distances":0.014447052718238582},{"index":861.0,"mean_distances":0.01419795245682066},{"index":862.0,"mean_distances":0.014197952456828034},{"index":863.0,"mean_distances":0.014322502587525975},{"index":864.0,"mean_distances":0.014322502587511826},{"index":865.0,"mean_distances":0.014076340670129145},{"index":866.0,"mean_distances":0.014076340670145982},{"index":867.0,"mean_distances":0.01444705271822492},{"index":868.0,"mean_distances":0.021915271822696522},{"index":869.0,"mean_distances":0.019094729648891327},{"index":870.0,"mean_distances":0.014447052718137352},{"index":871.0,"mean_distances":0.014447052718083607},{"index":872.0,"mean_distances":0.01432250258740648},{"index":873.0,"mean_distances":0.014322502587490038},{"index":874.0,"mean_distances":0.014447052718163302},{"index":875.0,"mean_distances":0.014197952456793297},{"index":876.0,"mean_distances":0.014197952456758747},{"index":877.0,"mean_distances":0.014322502587460676},{"index":878.0,"mean_distances":0.014322502587432383},{"index":879.0,"mean_distances":0.014076340670065607},{"index":880.0,"mean_distances":0.014076340670047443},{"index":881.0,"mean_distances":0.014447052718191099},{"index":882.0,"mean_distances":0.014322502587487134},{"index":883.0,"mean_distances":0.014322502587435402},{"index":884.0,"mean_distances":0.014447052718136462},{"index":885.0,"mean_distances":0.02191527182264255},{"index":886.0,"mean_distances":0.021422947987962116},{"index":887.0,"mean_distances":0.014447052718246171},{"index":888.0,"mean_distances":0.014447052718232316},{"index":889.0,"mean_distances":0.014322502587515428},{"index":890.0,"mean_distances":0.014322502587518333},{"index":891.0,"mean_distances":0.014447052718217527},{"index":892.0,"mean_distances":0.014197952456819726},{"index":893.0,"mean_distances":0.014197952456813405},{"index":894.0,"mean_distances":0.014322502587537402},{"index":895.0,"mean_distances":0.014322502587579842},{"index":896.0,"mean_distances":0.014076340670150489},{"index":897.0,"mean_distances":0.014076340670146471},{"index":898.0,"mean_distances":0.014447052718217527},{"index":899.0,"mean_distances":0.01432250258752746},{"index":900.0,"mean_distances":0.014322502587531023},{"index":901.0,"mean_distances":0.02154749811867518},{"index":902.0,"mean_distances":0.020891433610181726},{"index":903.0,"mean_distances":0.014447052718212361},{"index":904.0,"mean_distances":0.014447052718211707},{"index":905.0,"mean_distances":0.014322502587501283},{"index":906.0,"mean_distances":0.014322502587504187},{"index":907.0,"mean_distances":0.014447052718191099},{"index":908.0,"mean_distances":0.014197952456786225},{"index":909.0,"mean_distances":0.014197952456792907},{"index":910.0,"mean_distances":0.014322502587491966},{"index":911.0,"mean_distances":0.014322502587499038},{"index":912.0,"mean_distances":0.01407634067014329},{"index":913.0,"mean_distances":0.014076340670146471},{"index":914.0,"mean_distances":0.014447052718198046},{"index":915.0,"mean_distances":0.014322502587494084},{"index":916.0,"mean_distances":0.014322502587490038},{"index":917.0,"mean_distances":0.021015983740885688},{"index":918.0,"mean_distances":0.02142294798796728},{"index":919.0,"mean_distances":0.01444705271824377},{"index":920.0,"mean_distances":0.014447052718231752},{"index":921.0,"mean_distances":0.014322502587507299},{"index":922.0,"mean_distances":0.014322502587503701},{"index":923.0,"mean_distances":0.014447052718218091},{"index":924.0,"mean_distances":0.01419795245682066},{"index":925.0,"mean_distances":0.0141979524568212},{"index":926.0,"mean_distances":0.014322502587532369},{"index":927.0,"mean_distances":0.01432250258752883},{"index":928.0,"mean_distances":0.014076340670157436},{"index":929.0,"mean_distances":0.01407634067015659},{"index":930.0,"mean_distances":0.01444705271822492},{"index":931.0,"mean_distances":0.014322502587521444},{"index":932.0,"mean_distances":0.01432250258753151},{"index":933.0,"mean_distances":0.021547498118663685},{"index":934.0,"mean_distances":0.021422947987957797},{"index":935.0,"mean_distances":0.01444705271827349},{"index":936.0,"mean_distances":0.014447052718326392},{"index":937.0,"mean_distances":0.014322502587624375},{"index":938.0,"mean_distances":0.014322502587546625},{"index":939.0,"mean_distances":0.014447052718271755},{"index":940.0,"mean_distances":0.014197952456931034},{"index":941.0,"mean_distances":0.014197952456899249},{"index":942.0,"mean_distances":0.01432250258764786},{"index":943.0,"mean_distances":0.014322502587619565},{"index":944.0,"mean_distances":0.01407634067017878},{"index":945.0,"mean_distances":0.014076340670132323},{"index":946.0,"mean_distances":0.014447052718243958},{"index":947.0,"mean_distances":0.02191527182275871},{"index":948.0,"mean_distances":0.021422947987988248},{"index":949.0,"mean_distances":0.014447052718274464},{"index":950.0,"mean_distances":0.014447052718252478},{"index":951.0,"mean_distances":0.01432250258753559},{"index":952.0,"mean_distances":0.014322502587559316},{"index":953.0,"mean_distances":0.014447052718238582},{"index":954.0,"mean_distances":0.01419795245682066},{"index":955.0,"mean_distances":0.014197952456828034},{"index":956.0,"mean_distances":0.01432250258755155},{"index":957.0,"mean_distances":0.014322502587537402},{"index":958.0,"mean_distances":0.014076340670171337},{"index":959.0,"mean_distances":0.014076340670174275},{"index":960.0,"mean_distances":0.01444705271823882},{"index":961.0,"mean_distances":0.021915271822696522},{"index":962.0,"mean_distances":0.020566718696370476},{"index":963.0,"mean_distances":0.014568664504962497},{"index":964.0,"mean_distances":0.014322502587567787},{"index":965.0,"mean_distances":0.014322502587599336},{"index":966.0,"mean_distances":0.014447052718273533},{"index":967.0,"mean_distances":0.014197952456821593},{"index":968.0,"mean_distances":0.014197952456869991},{"index":969.0,"mean_distances":0.01432250258764786},{"index":970.0,"mean_distances":0.014693214635649508},{"index":971.0,"mean_distances":0.02166910990534091},{"index":972.0,"mean_distances":0.020196004685962072},{"index":973.0,"mean_distances":0.014447052718218853},{"index":974.0,"mean_distances":0.014447052718231426},{"index":975.0,"mean_distances":0.014322502587555755},{"index":976.0,"mean_distances":0.014322502587559316},{"index":977.0,"mean_distances":0.014447052718232316},{"index":978.0,"mean_distances":0.014197952456821593},{"index":979.0,"mean_distances":0.014197952456898283},{"index":980.0,"mean_distances":0.014322502587593988},{"index":981.0,"mean_distances":0.014693214635652227},{"index":982.0,"mean_distances":0.021669109905355772},{"index":983.0,"mean_distances":0.02007148884930809},{"index":984.0,"mean_distances":0.014076340670150239},{"index":985.0,"mean_distances":0.014076340670160128},{"index":986.0,"mean_distances":0.01444705271823187},{"index":987.0,"mean_distances":0.014322502587514246},{"index":988.0,"mean_distances":0.014322502587531023},{"index":989.0,"mean_distances":0.014447052718258744},{"index":990.0,"mean_distances":0.014197952456833874},{"index":991.0,"mean_distances":0.014197952456828034},{"index":992.0,"mean_distances":0.014322502587538763},{"index":993.0,"mean_distances":0.021558822677334156},{"index":994.0,"mean_distances":0.020442175679701653},{"index":995.0,"mean_distances":0.014693214635626006},{"index":996.0,"mean_distances":0.014322502587538763},{"index":997.0,"mean_distances":0.014076340670164384},{"index":998.0,"mean_distances":0.01407634067017379},{"index":999.0,"mean_distances":0.014447052718258744},{"index":1.0e3,"mean_distances":0.01432250258752746},{"index":1001.0,"mean_distances":0.014322502587531023},{"index":1002.0,"mean_distances":0.014447052718258744},{"index":1003.0,"mean_distances":0.014197952456833874},{"index":1004.0,"mean_distances":0.014197952456842182},{"index":1005.0,"mean_distances":0.01432250258755291},{"index":1006.0,"mean_distances":0.02155879927640114},{"index":1007.0,"mean_distances":0.021422947987855195},{"index":1008.0,"mean_distances":0.014447052718108535},{"index":1009.0,"mean_distances":0.014447052718191099},{"index":1010.0,"mean_distances":0.014322502587487134},{"index":1011.0,"mean_distances":0.014322502587435402},{"index":1012.0,"mean_distances":0.014447052718136462},{"index":1013.0,"mean_distances":0.014197952456765006},{"index":1014.0,"mean_distances":0.014197952456786074},{"index":1015.0,"mean_distances":0.014322502587483535},{"index":1016.0,"mean_distances":0.014693214635571493},{"index":1017.0,"mean_distances":0.021669109905304476},{"index":1018.0,"mean_distances":0.021052235939903654},{"index":1019.0,"mean_distances":0.01407634067019268},{"index":1020.0,"mean_distances":0.014076340670187934},{"index":1021.0,"mean_distances":0.014447052718258744},{"index":1022.0,"mean_distances":0.014322502587555755},{"index":1023.0,"mean_distances":0.014322502587559316},{"index":1024.0,"mean_distances":0.014447052718258744},{"index":1025.0,"mean_distances":0.014197952456862166},{"index":1026.0,"mean_distances":0.014197952456856329},{"index":1027.0,"mean_distances":0.014322502587554268},{"index":1028.0,"mean_distances":0.014693214635626652},{"index":1029.0,"mean_distances":0.021669109905369206},{"index":1030.0,"mean_distances":0.021793660036042713},{"index":1031.0,"mean_distances":0.014568664504895518},{"index":1032.0,"mean_distances":0.01419795245682066},{"index":1033.0,"mean_distances":0.014197952456828034},{"index":1034.0,"mean_distances":0.014322502587525975},{"index":1035.0,"mean_distances":0.014322502587533049},{"index":1036.0,"mean_distances":0.014076340670164384},{"index":1037.0,"mean_distances":0.014076340670167201},{"index":1038.0,"mean_distances":0.01444705271823187},{"index":1039.0,"mean_distances":0.014322502587528393},{"index":1040.0,"mean_distances":0.014322502587524677},{"index":1041.0,"mean_distances":0.014447052718245083},{"index":1042.0,"mean_distances":0.014568664504913688},{"index":1043.0,"mean_distances":0.021544559774626243},{"index":1044.0,"mean_distances":0.021793660036035997},{"index":1045.0,"mean_distances":0.014568664504895518},{"index":1046.0,"mean_distances":0.01419795245682066},{"index":1047.0,"mean_distances":0.014197952456828034},{"index":1048.0,"mean_distances":0.014322502587525975},{"index":1049.0,"mean_distances":0.014322502587525975},{"index":1050.0,"mean_distances":0.014076340670171585},{"index":1051.0,"mean_distances":0.014076340670174275},{"index":1052.0,"mean_distances":0.01444705271822492},{"index":1053.0,"mean_distances":0.014322502587507299},{"index":1054.0,"mean_distances":0.014322502587510532},{"index":1055.0,"mean_distances":0.01444705271822492},{"index":1056.0,"mean_distances":0.021915271822696522},{"index":1057.0,"mean_distances":0.02166617156131569},{"index":1058.0,"mean_distances":0.014197952456931034},{"index":1059.0,"mean_distances":0.014197952456899249},{"index":1060.0,"mean_distances":0.014322502587596708},{"index":1061.0,"mean_distances":0.014322502587568413},{"index":1062.0,"mean_distances":0.014076340670206577},{"index":1063.0,"mean_distances":0.01407634067018696},{"index":1064.0,"mean_distances":0.014447052718326392},{"index":1065.0,"mean_distances":0.014322502587624375},{"index":1066.0,"mean_distances":0.014322502587573956},{"index":1067.0,"mean_distances":0.02154749811867998},{"index":1068.0,"mean_distances":0.0214229479879952},{"index":1069.0,"mean_distances":0.014447052718288349},{"index":1070.0,"mean_distances":0.014447052718299961},{"index":1071.0,"mean_distances":0.01419795245684802},{"index":1072.0,"mean_distances":0.014197952456856329},{"index":1073.0,"mean_distances":0.014322502587565697},{"index":1074.0,"mean_distances":0.014322502587579842},{"index":1075.0,"mean_distances":0.014076340670164387},{"index":1076.0,"mean_distances":0.014076340670146471},{"index":1077.0,"mean_distances":0.014447052718231426},{"index":1078.0,"mean_distances":0.014322502587555755},{"index":1079.0,"mean_distances":0.014322502587559316},{"index":1080.0,"mean_distances":0.021547498118684293},{"index":1081.0,"mean_distances":0.021422947987981302},{"index":1082.0,"mean_distances":0.014447052718254088},{"index":1083.0,"mean_distances":0.01444705271823187},{"index":1084.0,"mean_distances":0.014322502587521444},{"index":1085.0,"mean_distances":0.014322502587524677},{"index":1086.0,"mean_distances":0.01444705271822492},{"index":1087.0,"mean_distances":0.01419795245682066},{"index":1088.0,"mean_distances":0.014197952456828034},{"index":1089.0,"mean_distances":0.014322502587538763},{"index":1090.0,"mean_distances":0.014322502587524615},{"index":1091.0,"mean_distances":0.014076340670150239},{"index":1092.0,"mean_distances":0.014076340670160128},{"index":1093.0,"mean_distances":0.01444705271823187},{"index":1094.0,"mean_distances":0.014322502587514246},{"index":1095.0,"mean_distances":0.014322502587531023},{"index":1096.0,"mean_distances":0.021547498118684293},{"index":1097.0,"mean_distances":0.021422947987967154},{"index":1098.0,"mean_distances":0.014447052718233225},{"index":1099.0,"mean_distances":0.014447052718245083},{"index":1.1e3,"mean_distances":0.014322502587541606},{"index":1101.0,"mean_distances":0.01432250258753151},{"index":1102.0,"mean_distances":0.014447052718245083},{"index":1103.0,"mean_distances":0.014197952456855093},{"index":1104.0,"mean_distances":0.014197952456849254},{"index":1105.0,"mean_distances":0.014322502587540122},{"index":1106.0,"mean_distances":0.014322502587536584},{"index":1107.0,"mean_distances":0.01407634067017146},{"index":1108.0,"mean_distances":0.014076340670177323},{"index":1109.0,"mean_distances":0.014447052718258744},{"index":1110.0,"mean_distances":0.014322502587541606},{"index":1111.0,"mean_distances":0.014322502587541752},{"index":1112.0,"mean_distances":0.021547498118684293},{"index":1113.0,"mean_distances":0.021793660036099515},{"index":1114.0,"mean_distances":0.014568664504962475},{"index":1115.0,"mean_distances":0.014322502587624375},{"index":1116.0,"mean_distances":0.014322502587546625},{"index":1117.0,"mean_distances":0.014447052718271755},{"index":1118.0,"mean_distances":0.014197952456931034},{"index":1119.0,"mean_distances":0.014197952456899249},{"index":1120.0,"mean_distances":0.014322502587596708},{"index":1121.0,"mean_distances":0.014322502587483535},{"index":1122.0,"mean_distances":0.014076340670122194},{"index":1123.0,"mean_distances":0.01407634067010403},{"index":1124.0,"mean_distances":0.014447052718243958},{"index":1125.0,"mean_distances":0.014322502587567787},{"index":1126.0,"mean_distances":0.014322502587599336},{"index":1127.0,"mean_distances":0.014447052718273533},{"index":1128.0,"mean_distances":0.014568664504879827},{"index":1129.0,"mean_distances":0.021544559774639427},{"index":1130.0,"mean_distances":0.0217936600360451},{"index":1131.0,"mean_distances":0.014568664504882298},{"index":1132.0,"mean_distances":0.014322502587515428},{"index":1133.0,"mean_distances":0.014322502587518333},{"index":1134.0,"mean_distances":0.014447052718191099},{"index":1135.0,"mean_distances":0.014197952456786225},{"index":1136.0,"mean_distances":0.014197952456792907},{"index":1137.0,"mean_distances":0.014322502587504754},{"index":1138.0,"mean_distances":0.014322502587511826},{"index":1139.0,"mean_distances":0.014076340670150239},{"index":1140.0,"mean_distances":0.014076340670146471},{"index":1141.0,"mean_distances":0.014447052718204997},{"index":1142.0,"mean_distances":0.014322502587501033},{"index":1143.0,"mean_distances":0.014322502587490038},{"index":1144.0,"mean_distances":0.014447052718231426},{"index":1145.0,"mean_distances":0.014568664504892824},{"index":1146.0,"mean_distances":0.02154455977460071},{"index":1147.0,"mean_distances":0.021422947988032598},{"index":1148.0,"mean_distances":0.01444705271827544},{"index":1149.0,"mean_distances":0.014447052718218896},{"index":1150.0,"mean_distances":0.014322502587543721},{"index":1151.0,"mean_distances":0.014322502587628592},{"index":1152.0,"mean_distances":0.014447052718298594},{"index":1153.0,"mean_distances":0.014197952456931034},{"index":1154.0,"mean_distances":0.014197952456899249},{"index":1155.0,"mean_distances":0.014322502587596708},{"index":1156.0,"mean_distances":0.014322502587568413},{"index":1157.0,"mean_distances":0.014076340670206577},{"index":1158.0,"mean_distances":0.01407634067018696},{"index":1159.0,"mean_distances":0.014447052718326392},{"index":1160.0,"mean_distances":0.014322502587624375},{"index":1161.0,"mean_distances":0.014322502587573956},{"index":1162.0,"mean_distances":0.014447052718271755},{"index":1163.0,"mean_distances":0.02191527182274049},{"index":1164.0,"mean_distances":0.021422947987939107},{"index":1165.0,"mean_distances":0.01444705271820542},{"index":1166.0,"mean_distances":0.014447052718191099},{"index":1167.0,"mean_distances":0.014322502587487134},{"index":1168.0,"mean_distances":0.014322502587490038},{"index":1169.0,"mean_distances":0.014447052718191099},{"index":1170.0,"mean_distances":0.01419795245675086},{"index":1171.0,"mean_distances":0.014197952456743155},{"index":1172.0,"mean_distances":0.014322502587469388},{"index":1173.0,"mean_distances":0.014322502587497682},{"index":1174.0,"mean_distances":0.014076340670122194},{"index":1175.0,"mean_distances":0.014076340670118176},{"index":1176.0,"mean_distances":0.014447052718191099},{"index":1177.0,"mean_distances":0.014322502587487134},{"index":1178.0,"mean_distances":0.014322502587490038},{"index":1179.0,"mean_distances":0.021547498118633962},{"index":1180.0,"mean_distances":0.021422947987967154},{"index":1181.0,"mean_distances":0.014447052718246886},{"index":1182.0,"mean_distances":0.01444705271824553},{"index":1183.0,"mean_distances":0.01432250258753559},{"index":1184.0,"mean_distances":0.014322502587538824},{"index":1185.0,"mean_distances":0.01444705271822492},{"index":1186.0,"mean_distances":0.01419795245682066},{"index":1187.0,"mean_distances":0.014197952456828034},{"index":1188.0,"mean_distances":0.014322502587525975},{"index":1189.0,"mean_distances":0.014322502587533049},{"index":1190.0,"mean_distances":0.014076340670164384},{"index":1191.0,"mean_distances":0.014076340670167201},{"index":1192.0,"mean_distances":0.01444705271823187},{"index":1193.0,"mean_distances":0.014568664504893756},{"index":1194.0,"mean_distances":0.021544559774623967},{"index":1195.0,"mean_distances":0.021422947987960208},{"index":1196.0,"mean_distances":0.014447052718226508},{"index":1197.0,"mean_distances":0.01444705271822492},{"index":1198.0,"mean_distances":0.014322502587507299},{"index":1199.0,"mean_distances":0.014322502587496871},{"index":1.2e3,"mean_distances":0.014447052718211261},{"index":1201.0,"mean_distances":0.01419795245682066},{"index":1202.0,"mean_distances":0.014197952456814128},{"index":1203.0,"mean_distances":0.014322502587518902},{"index":1204.0,"mean_distances":0.014322502587515364},{"index":1205.0,"mean_distances":0.014076340670150364},{"index":1206.0,"mean_distances":0.01407634067015659},{"index":1207.0,"mean_distances":0.01444705271822492},{"index":1208.0,"mean_distances":0.014568664504893756},{"index":1209.0,"mean_distances":0.021544559774627384},{"index":1210.0,"mean_distances":0.021790721691986148},{"index":1211.0,"mean_distances":0.014322502587543721},{"index":1212.0,"mean_distances":0.014322502587628592},{"index":1213.0,"mean_distances":0.014447052718298594},{"index":1214.0,"mean_distances":0.014197952456931034},{"index":1215.0,"mean_distances":0.014197952456899249},{"index":1216.0,"mean_distances":0.014322502587596708},{"index":1217.0,"mean_distances":0.014322502587568413},{"index":1218.0,"mean_distances":0.014076340670206577},{"index":1219.0,"mean_distances":0.01407634067018696},{"index":1220.0,"mean_distances":0.014447052718326392},{"index":1221.0,"mean_distances":0.014322502587624375},{"index":1222.0,"mean_distances":0.014322502587573956},{"index":1223.0,"mean_distances":0.014447052718271755},{"index":1224.0,"mean_distances":0.02191527182274049},{"index":1225.0,"mean_distances":0.021422947987985858},{"index":1226.0,"mean_distances":0.01444705271826103},{"index":1227.0,"mean_distances":0.014447052718258744},{"index":1228.0,"mean_distances":0.014322502587555755},{"index":1229.0,"mean_distances":0.014322502587559316},{"index":1230.0,"mean_distances":0.014447052718258744},{"index":1231.0,"mean_distances":0.014197952456855093},{"index":1232.0,"mean_distances":0.01419795245686316},{"index":1233.0,"mean_distances":0.014322502587547194},{"index":1234.0,"mean_distances":0.014322502587554268},{"index":1235.0,"mean_distances":0.014076340670178532},{"index":1236.0,"mean_distances":0.014076340670187934},{"index":1237.0,"mean_distances":0.014447052718258744},{"index":1238.0,"mean_distances":0.014568664504927832},{"index":1239.0,"mean_distances":0.02154455977464495},{"index":1240.0,"mean_distances":0.016740786949730163},{"index":1241.0,"mean_distances":0.011640004315665217},{"index":1242.0,"mean_distances":0.011393842398348683},{"index":1243.0,"mean_distances":0.011764554446325454},{"index":1244.0,"mean_distances":0.011764554446426717},{"index":1245.0,"mean_distances":0.011393842398304009},{"index":1246.0,"mean_distances":0.011518392528949435},{"index":1247.0,"mean_distances":0.011764554446310643},{"index":1248.0,"mean_distances":0.011640004315653305},{"index":1249.0,"mean_distances":0.01151839252899411},{"index":1250.0,"mean_distances":0.011764554446310643},{"index":1251.0,"mean_distances":0.011640004315608632},{"index":1252.0,"mean_distances":0.011393842398247422},{"index":1253.0,"mean_distances":0.013534752154809418},{"index":1254.0,"mean_distances":0.013604999287636301},{"index":1255.0,"mean_distances":0.011496460322157946},{"index":1256.0,"mean_distances":0.011250298404789666},{"index":1257.0,"mean_distances":0.011621010452875622},{"index":1258.0,"mean_distances":0.011621010452927003},{"index":1259.0,"mean_distances":0.011250298404846253},{"index":1260.0,"mean_distances":0.011374848535549242},{"index":1261.0,"mean_distances":0.011621010452889229},{"index":1262.0,"mean_distances":0.011496460322209327},{"index":1263.0,"mean_distances":0.011374848535526153},{"index":1264.0,"mean_distances":0.011621010452889229},{"index":1265.0,"mean_distances":0.011496460322209327},{"index":1266.0,"mean_distances":0.011250298404846253},{"index":1267.0,"mean_distances":0.01327926121554028},{"index":1268.0,"mean_distances":0.013866022771853207},{"index":1269.0,"mean_distances":0.011644002156489612},{"index":1270.0,"mean_distances":0.011397840239125602},{"index":1271.0,"mean_distances":0.011768552287194927},{"index":1272.0,"mean_distances":0.011768552287180779},{"index":1273.0,"mean_distances":0.011397840239097309},{"index":1274.0,"mean_distances":0.01152239036981493},{"index":1275.0,"mean_distances":0.011768552287193089},{"index":1276.0,"mean_distances":0.011644002156475463},{"index":1277.0,"mean_distances":0.011522390369828592},{"index":1278.0,"mean_distances":0.011768552287206746},{"index":1279.0,"mean_distances":0.011644002156489612},{"index":1280.0,"mean_distances":0.013541888344310646},{"index":1281.0,"mean_distances":0.015385488960446309},{"index":1282.0,"mean_distances":0.012487721350519959},{"index":1283.0,"mean_distances":0.012241559433133367},{"index":1284.0,"mean_distances":0.01261227148120133},{"index":1285.0,"mean_distances":0.012612271481224848},{"index":1286.0,"mean_distances":0.012241559433147515},{"index":1287.0,"mean_distances":0.012366109563850503},{"index":1288.0,"mean_distances":0.012612271481213577},{"index":1289.0,"mean_distances":0.012487721350510588},{"index":1290.0,"mean_distances":0.012366109563850503},{"index":1291.0,"mean_distances":0.01261227148122295},{"index":1292.0,"mean_distances":0.012487721350510588},{"index":1293.0,"mean_distances":0.017026095209651388},{"index":1294.0,"mean_distances":0.02030664196353577},{"index":1295.0,"mean_distances":0.014322502587544611},{"index":1296.0,"mean_distances":0.014322502587517263},{"index":1297.0,"mean_distances":0.014322502587432383},{"index":1298.0,"mean_distances":0.014076340670122194},{"index":1299.0,"mean_distances":0.01407634067010403},{"index":1.3e3,"mean_distances":0.014447052718243958},{"index":1301.0,"mean_distances":0.014322502587567787},{"index":1302.0,"mean_distances":0.014322502587435402},{"index":1303.0,"mean_distances":0.014447052718164259},{"index":1304.0,"mean_distances":0.014568664504852962},{"index":1305.0,"mean_distances":0.020552803880893488},{"index":1306.0,"mean_distances":0.021666171561262836},{"index":1307.0,"mean_distances":0.01419795245677915},{"index":1308.0,"mean_distances":0.014197952456786074},{"index":1309.0,"mean_distances":0.014322502587497682},{"index":1310.0,"mean_distances":0.014322502587511826},{"index":1311.0,"mean_distances":0.014076340670093902},{"index":1312.0,"mean_distances":0.01407634067007671},{"index":1313.0,"mean_distances":0.01444705271816378},{"index":1314.0,"mean_distances":0.014322502587487134},{"index":1315.0,"mean_distances":0.014322502587490038},{"index":1316.0,"mean_distances":0.01444705271816467},{"index":1317.0,"mean_distances":0.014568664504839969},{"index":1318.0,"mean_distances":0.021544559774607546},{"index":1319.0,"mean_distances":0.020800159119944962},{"index":1320.0,"mean_distances":0.014197952456813587},{"index":1321.0,"mean_distances":0.014197952456807056},{"index":1322.0,"mean_distances":0.014322502587504754},{"index":1323.0,"mean_distances":0.014322502587533049},{"index":1324.0,"mean_distances":0.014076340670164384},{"index":1325.0,"mean_distances":0.014076340670167201},{"index":1326.0,"mean_distances":0.01444705271823187},{"index":1327.0,"mean_distances":0.014322502587528393},{"index":1328.0,"mean_distances":0.014322502587524677},{"index":1329.0,"mean_distances":0.014447052718245083},{"index":1330.0,"mean_distances":0.01456866450490697},{"index":1331.0,"mean_distances":0.020553997202587788},{"index":1332.0,"mean_distances":0.021666171561278272},{"index":1333.0,"mean_distances":0.01419795245682066},{"index":1334.0,"mean_distances":0.0141979524568212},{"index":1335.0,"mean_distances":0.014322502587525975},{"index":1336.0,"mean_distances":0.014322502587504754},{"index":1337.0,"mean_distances":0.014076340670129145},{"index":1338.0,"mean_distances":0.01407634067013891},{"index":1339.0,"mean_distances":0.01444705271822492},{"index":1340.0,"mean_distances":0.014322502587507299},{"index":1341.0,"mean_distances":0.014322502587517364},{"index":1342.0,"mean_distances":0.01444705271822492},{"index":1343.0,"mean_distances":0.021915271822689805},{"index":1344.0,"mean_distances":0.02152765211449761},{"index":1345.0,"mean_distances":0.014197952456849884},{"index":1346.0,"mean_distances":0.01419795245684266},{"index":1347.0,"mean_distances":0.014322502587511826},{"index":1348.0,"mean_distances":0.014322502587568413},{"index":1349.0,"mean_distances":0.01407634067017878},{"index":1350.0,"mean_distances":0.014076340670132323},{"index":1351.0,"mean_distances":0.021284428541172754},{"index":1352.0,"mean_distances":0.021793660036063086},{"index":1353.0,"mean_distances":0.014568664504936053},{"index":1354.0,"mean_distances":0.014197952456819726},{"index":1355.0,"mean_distances":0.014197952456813405},{"index":1356.0,"mean_distances":0.014322502587537402},{"index":1357.0,"mean_distances":0.014322502587565697},{"index":1358.0,"mean_distances":0.014322502587571477},{"index":1359.0,"mean_distances":0.021298397857282676},{"index":1360.0,"mean_distances":0.021162568315432104},{"index":1361.0,"mean_distances":0.014447052718233225},{"index":1362.0,"mean_distances":0.01444705271822492},{"index":1363.0,"mean_distances":0.01419795245682066},{"index":1364.0,"mean_distances":0.014197952456828034},{"index":1365.0,"mean_distances":0.014322502587538763},{"index":1366.0,"mean_distances":0.014693214635597715},{"index":1367.0,"mean_distances":0.02140873023279027},{"index":1368.0,"mean_distances":0.02179072169198684},{"index":1369.0,"mean_distances":0.014322502587524918},{"index":1370.0,"mean_distances":0.014322502587528091},{"index":1371.0,"mean_distances":0.014447052718228395},{"index":1372.0,"mean_distances":0.01419795245682066},{"index":1373.0,"mean_distances":0.0141979524568212},{"index":1374.0,"mean_distances":0.014322502587532369},{"index":1375.0,"mean_distances":0.014693214635608824},{"index":1376.0,"mean_distances":0.021669109905338154},{"index":1377.0,"mean_distances":0.021422947987957797},{"index":1378.0,"mean_distances":0.01444705271827349},{"index":1379.0,"mean_distances":0.014447052718273533},{"index":1380.0,"mean_distances":0.014322502587487134},{"index":1381.0,"mean_distances":0.014322502587490038},{"index":1382.0,"mean_distances":0.014447052718243958},{"index":1383.0,"mean_distances":0.014197952456846153},{"index":1384.0,"mean_distances":0.01419795245684266},{"index":1385.0,"mean_distances":0.014322502587517263},{"index":1386.0,"mean_distances":0.014322502587432383},{"index":1387.0,"mean_distances":0.014076340670122194},{"index":1388.0,"mean_distances":0.01407634067010403},{"index":1389.0,"mean_distances":0.014447052718243958},{"index":1390.0,"mean_distances":0.014322502587567787},{"index":1391.0,"mean_distances":0.014322502587435402},{"index":1392.0,"mean_distances":0.021547498118607122},{"index":1393.0,"mean_distances":0.021422947987974103},{"index":1394.0,"mean_distances":0.014447052718253603},{"index":1395.0,"mean_distances":0.014447052718252478},{"index":1396.0,"mean_distances":0.01432250258753559},{"index":1397.0,"mean_distances":0.014322502587538824},{"index":1398.0,"mean_distances":0.01444705271822492},{"index":1399.0,"mean_distances":0.01419795245682066},{"index":1.4e3,"mean_distances":0.014197952456828034},{"index":1401.0,"mean_distances":0.01432250258755155},{"index":1402.0,"mean_distances":0.014322502587537402},{"index":1403.0,"mean_distances":0.014076340670171337},{"index":1404.0,"mean_distances":0.014076340670174275},{"index":1405.0,"mean_distances":0.01444705271823882},{"index":1406.0,"mean_distances":0.014322502587521197},{"index":1407.0,"mean_distances":0.014322502587531023},{"index":1408.0,"mean_distances":0.02154749811869124},{"index":1409.0,"mean_distances":0.017931353015655568},{"index":1410.0,"mean_distances":0.014443405380787385},{"index":1411.0,"mean_distances":0.014447052718191099},{"index":1412.0,"mean_distances":0.014322502587487134},{"index":1413.0,"mean_distances":0.014322502587490038},{"index":1414.0,"mean_distances":0.014447052718191099},{"index":1415.0,"mean_distances":0.014197952456849884},{"index":1416.0,"mean_distances":0.01419795245684266},{"index":1417.0,"mean_distances":0.014322502587511826},{"index":1418.0,"mean_distances":0.014322502587568413},{"index":1419.0,"mean_distances":0.01407634067017878},{"index":1420.0,"mean_distances":0.014076340670132323},{"index":1421.0,"mean_distances":0.014447052718191099},{"index":1422.0,"mean_distances":0.014322502587487134},{"index":1423.0,"mean_distances":0.014322502587517369},{"index":1424.0,"mean_distances":0.01805590314635953},{"index":1425.0,"mean_distances":0.021422947987981302},{"index":1426.0,"mean_distances":0.01444705271826103},{"index":1427.0,"mean_distances":0.014447052718258744},{"index":1428.0,"mean_distances":0.014322502587569653},{"index":1429.0,"mean_distances":0.014322502587586635},{"index":1430.0,"mean_distances":0.014447052718299961},{"index":1431.0,"mean_distances":0.01419795245684802},{"index":1432.0,"mean_distances":0.014197952456856329},{"index":1433.0,"mean_distances":0.014322502587565697},{"index":1434.0,"mean_distances":0.014322502587579842},{"index":1435.0,"mean_distances":0.014076340670164387},{"index":1436.0,"mean_distances":0.014076340670146471},{"index":1437.0,"mean_distances":0.014447052718231426},{"index":1438.0,"mean_distances":0.014322502587555755},{"index":1439.0,"mean_distances":0.014322502587559316},{"index":1440.0,"mean_distances":0.021547498118684293},{"index":1441.0,"mean_distances":0.017934392268561927},{"index":1442.0,"mean_distances":0.014446444633693503},{"index":1443.0,"mean_distances":0.01444705271823187},{"index":1444.0,"mean_distances":0.014322502587521444},{"index":1445.0,"mean_distances":0.014322502587524677},{"index":1446.0,"mean_distances":0.01444705271822492},{"index":1447.0,"mean_distances":0.01419795245682066},{"index":1448.0,"mean_distances":0.014197952456828034},{"index":1449.0,"mean_distances":0.014322502587538763},{"index":1450.0,"mean_distances":0.014322502587524615},{"index":1451.0,"mean_distances":0.014076340670150239},{"index":1452.0,"mean_distances":0.014076340670160128},{"index":1453.0,"mean_distances":0.01444705271823187},{"index":1454.0,"mean_distances":0.014322502587514246},{"index":1455.0,"mean_distances":0.014322502587531023},{"index":1456.0,"mean_distances":0.01805894239927906},{"index":1457.0,"mean_distances":0.02142294798796368},{"index":1458.0,"mean_distances":0.014447052718229866},{"index":1459.0,"mean_distances":0.014447052718235003},{"index":1460.0,"mean_distances":0.014322502587524454},{"index":1461.0,"mean_distances":0.014322502587514191},{"index":1462.0,"mean_distances":0.014447052718228173},{"index":1463.0,"mean_distances":0.014197952456827269},{"index":1464.0,"mean_distances":0.014197952456824614},{"index":1465.0,"mean_distances":0.014322502587525975},{"index":1466.0,"mean_distances":0.014322502587525975},{"index":1467.0,"mean_distances":0.01407634067016091},{"index":1468.0,"mean_distances":0.014076340670166958},{"index":1469.0,"mean_distances":0.014447052718241834},{"index":1470.0,"mean_distances":0.014322502587524454},{"index":1471.0,"mean_distances":0.014322502587510777},{"index":1472.0,"mean_distances":0.02154749811865805},{"index":1473.0,"mean_distances":0.019094729648975715},{"index":1474.0,"mean_distances":0.014447052718330076},{"index":1475.0,"mean_distances":0.014447052718326392},{"index":1476.0,"mean_distances":0.014322502587624375},{"index":1477.0,"mean_distances":0.014322502587628592},{"index":1478.0,"mean_distances":0.014447052718326392},{"index":1479.0,"mean_distances":0.014197952456987623},{"index":1480.0,"mean_distances":0.014197952456983166},{"index":1481.0,"mean_distances":0.01432250258764786},{"index":1482.0,"mean_distances":0.014322502587704447},{"index":1483.0,"mean_distances":0.014076340670319753},{"index":1484.0,"mean_distances":0.01407634067027184},{"index":1485.0,"mean_distances":0.014447052718326392},{"index":1486.0,"mean_distances":0.019587053483678615},{"index":1487.0,"mean_distances":0.02089143361020282},{"index":1488.0,"mean_distances":0.014447052718233225},{"index":1489.0,"mean_distances":0.01444705271823187},{"index":1490.0,"mean_distances":0.014322502587521444},{"index":1491.0,"mean_distances":0.014322502587524677},{"index":1492.0,"mean_distances":0.01444705271822492},{"index":1493.0,"mean_distances":0.01419795245682066},{"index":1494.0,"mean_distances":0.014197952456828034},{"index":1495.0,"mean_distances":0.014322502587538763},{"index":1496.0,"mean_distances":0.014322502587524615},{"index":1497.0,"mean_distances":0.014076340670150239},{"index":1498.0,"mean_distances":0.014076340670160128},{"index":1499.0,"mean_distances":0.01444705271823187},{"index":1.5e3,"mean_distances":0.014322502587514246},{"index":1501.0,"mean_distances":0.014322502587531023},{"index":1502.0,"mean_distances":0.021015983740919956}]},"height":630,"layer":[{"encoding":{"x":{"field":"index","scale":{"domain":[0,1510]},"type":"quantitative"},"y":{"field":"mean_distances","scale":{"domain":[0.0085,0.0225]},"type":"quantitative"}},"mark":{"color":"jet","fillOpacity":1,"type":"line"}},{"encoding":{"y":{"datum":0.018,"scale":{"domain":[0.0085,0.0225]}}},"mark":{"color":"red","strokeDash":[5,5],"strokeWidth":1,"type":"rule"}}],"title":{"offset":20,"text":"Plot to check anomalies"},"width":800}

We can assume, that samples with average distance bigger than 0.018 can be treated as outliers.

data = DF.put(data, :is_outlier, Nx.greater(mean_distances, 0.018))

#Explorer.DataFrame<
  Polars[1503 x 6]
  angle_of_attack f64 [0.0, 0.0, 0.0, 0.0, 0.0, ...]
  chord_length f64 [0.3048, 0.3048, 0.3048, 0.3048, 0.3048, ...]
  free_stream_velocity f64 [71.3, 71.3, 71.3, 71.3, 71.3, ...]
  frequency_log f64 [6.684611727667927, 6.907755278982137, 7.1308988302963465, 7.3777589082278725, 7.600902459542082, ...]
  suction_side_displacement_thickness_log f64 [-5.928163040757819, -5.928163040757819, -5.928163040757819, -5.928163040757819, -5.928163040757819, ...]
  is_outlier u8 [1, 0, 0, 0, 0, ...]
>

alias VegaLite, as: Vl

Vl.new(
  title: [
    text: "Logarithm of Frequency vs Logarithm of Suction Side Displacement Thickness",
    offset: 20
  ],
  width: 630,
  height: 630
)
|> Vl.data_from_values(data)
|> Vl.layers([
  Vl.new()
  |> Vl.param("brush", select: :interval)
  |> Vl.mark(:circle)
  |> Vl.encode_field(:x, "frequency_log", type: :quantitative, scale: [domain: [4.5, 10.5]])
  |> Vl.encode_field(:y, "suction_side_displacement_thickness_log",
    type: :quantitative,
    scale: [domain: [-8.0, -2.5]]
  )
  |> Vl.encode(:color,
    condition: [param: "brush", field: "is_outlier", type: :nominal],
    value: :gray
  ),
  Vl.new()
  |> Vl.transform(filter: [param: "brush", field: "is_outlier", equal: true])
  |> Vl.mark(:text)
  |> Vl.encode(:x, value: 11)
  |> Vl.encode(:y, value: -3.5)
  |> Vl.encode_field(:text, "filter",
    type: :quantitative,
    aggregate: :count
  )
])

{"$schema":"https://vega.github.io/schema/vega-lite/v5.json","data":{"values":[{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-5.928163040757819},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-5.8671923891985855},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-5.775908105255605},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":0.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-5.710003786949502},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":1,"suction_side_displacement_thickness_log":-5.6936470124260525},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":1.5,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-5.541390703242673},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-5.4591271692002525},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-5.3981553815445436},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-5.306871852046764},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":3.0,"chord_length":0.3048,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":1,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-5.302781315157766},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":4.0,"chord_length":0.3048,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.150525144651317},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.903487552536127,"is_outlier":0,"suction_side_displacement_thickness_log":-6.145338598533738},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.077737287865621},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.977518250375487},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":0.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.905727314829417},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-5.832647059502022},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.765046363260115},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.664829104928296},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":2.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.593034795854161},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.903487552536127,"is_outlier":1,"suction_side_displacement_thickness_log":-5.519954552999701},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-5.452354719463699},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-5.352138062652583},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":1,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":4.0,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.280343862057888},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-5.260212660514491},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":5.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.092394849710159},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.562072383085368},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-4.49446995203478},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.394253073897531},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":7.3,"chord_length":0.2286,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-4.322460455162869},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-6.438501931127106},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-6.361554789400947},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.248749333992177},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":0.0,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.16865528907292},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":1,"suction_side_displacement_thickness_log":-6.016368081940886},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":1,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":2.7,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-5.826614736226067},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.518467901407987},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-5.441522831045896},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.328716782005891},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":5.4,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.248624752566102},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-4.8901372806630325},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":7.2,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-4.700387870070277},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.94764500173757},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.8706987370685173},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.7578951830049734},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":9.9,"chord_length":0.1524,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.6778010469069353},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.0299945799490042},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":12.6,"chord_length":0.1524,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-2.840245914714656},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-7.208214634353399},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-7.1796558700143995},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-7.141173938884094},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":0.0,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-7.115808267752531},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":1,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":1,"suction_side_displacement_thickness_log":-6.551564452209211},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":1,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":4.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-6.484522292013623},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":1,"suction_side_displacement_thickness_log":-5.240965860240528},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":1,"suction_side_displacement_thickness_log":-5.2124075961041525},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-5.1739268749534055},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":8.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-5.148560324627482},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-4.26356827154688},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":11.2,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-4.1965234778744955},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-3.633372848202307},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.604814078996269},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.56633267202546},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":15.4,"chord_length":0.0508,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.5409664740628757},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-3.3779213817499816},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":19.7,"chord_length":0.0508,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-3.310881470664225},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":1,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.903487552536127,"is_outlier":1,"suction_side_displacement_thickness_log":-7.822342462718742},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":1,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.903487552536127,"is_outlier":1,"suction_side_displacement_thickness_log":-7.793783572729404},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":1,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":9.680344001221918,"is_outlier":1,"suction_side_displacement_thickness_log":-7.755303837458148},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":1,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":0.0,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":9.680344001221918,"is_outlier":1,"suction_side_displacement_thickness_log":-7.729936551628486},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":1,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.903487552536127,"is_outlier":1,"suction_side_displacement_thickness_log":-7.071883738372609},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":1,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.680344001221918,"is_outlier":0,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":9.903487552536127,"is_outlier":1,"suction_side_displacement_thickness_log":-7.043325319666774},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":1,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-7.004844540414093},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":1,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":4.8,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-6.979477944397115},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.471114821925546},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.442557320266781},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.404075739118207},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":9.5,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-5.378709968760862},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":1,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-4.407894337412326},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":1,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":12.7,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-4.340861658978395},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-4.128687590644646},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-4.1001252381811275},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":1,"suction_side_displacement_thickness_log":-4.061648937383988},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":17.4,"chord_length":0.0254,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":1,"suction_side_displacement_thickness_log":-4.03627756127246},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-3.843532926987103},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":22.2,"chord_length":0.0254,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":1,"suction_side_displacement_thickness_log":-3.776496105154043},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.716540055018062},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":9.433483923290392,"is_outlier":0,"suction_side_displacement_thickness_log":-6.630252338556517},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.52704745222199},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":0.0,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":9.210340371976184,"is_outlier":0,"suction_side_displacement_thickness_log":-6.501677025552656},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":1,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-6.200596717874539},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-6.114310377106828},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.987196820661973,"is_outlier":0,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":9.210340371976184,"is_outlier":1,"suction_side_displacement_thickness_log":-6.011104147693738},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":0,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":3.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.987196820661973,"is_outlier":1,"suction_side_displacement_thickness_log":-5.985740958138386},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":1,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":1,"suction_side_displacement_thickness_log":-5.342712403455074},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":1,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":1,"suction_side_displacement_thickness_log":-5.256427142787852},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":1,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":1,"suction_side_displacement_thickness_log":-5.153220117052352},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":1,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":6.7,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":1,"suction_side_displacement_thickness_log":-5.1278541764170615},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-4.574757379579896},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":8.9,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-4.385263868866866},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.3879100505353783},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":55.5,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.3016244819896103},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.1984165504668303},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":12.3,"chord_length":0.1016,"free_stream_velocity":31.7,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-3.1730519605813474},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":71.3,"frequency_log":8.294049640102028,"is_outlier":1,"suction_side_displacement_thickness_log":-3.129814675098908},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.298317366548036,"is_outlier":1,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.521460917862246,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.752572638825633,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":5.991464547107982,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.214608098422191,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.4457198193855785,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.684611727667927,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":6.907755278982137,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.1308988302963465,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.3777589082278725,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.600902459542082,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":7.824046010856292,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.055157731819678,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.294049640102028,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.517193191416238,"is_outlier":0,"suction_side_displacement_thickness_log":-2.940322164887062},{"angle_of_attack":15.6,"chord_length":0.1016,"free_stream_velocity":39.6,"frequency_log":8.748304912379623,"is_outlier":1,"suction_side_displacement_thickness_log":-2.940322164887062}]},"height":630,"layer":[{"encoding":{"color":{"condition":{"field":"is_outlier","param":"brush","type":"nominal"},"value":"gray"},"x":{"field":"frequency_log","scale":{"domain":[4.5,10.5]},"type":"quantitative"},"y":{"field":"suction_side_displacement_thickness_log","scale":{"domain":[-8.0,-2.5]},"type":"quantitative"}},"mark":"circle","params":[{"name":"brush","select":"interval"}]},{"encoding":{"text":{"aggregate":"count","field":"filter","type":"quantitative"},"x":{"value":11},"y":{"value":-3.5}},"mark":"text","transform":[{"filter":{"equal":true,"field":"is_outlier","param":"brush"}}]}],"title":{"offset":20,"text":"Logarithm of Frequency vs Logarithm of Suction Side Displacement Thickness"},"width":630}